


Next: Rosenblum
Up: Abstracts
Previous: Robnik
Introduction to computational algebra
Valery Romanovski
Center for Applied Mathematics and Theoretical Physics,
University of Maribor, Maribor, Slovenia
Consider a system of polynomials
where 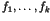 are polynomials with coefficients from
some field
are polynomials with coefficients from
some field 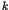 (usually,
(usually, 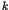 is the field of real or complex numbers).
In algebraic geometry the solution space of system (1) is called
the variety. There are many numerical algorithms for solving
non-linear systems such as (1). These algorithms solve for one solution
at a time, and find an approximation to the solution.
They ignore the geometric properties of the solutions space (the
variety),
and do not take into consideration possible alternate descriptions of
the variety (using a different system of polynomials).
However recently efficient computational algorithms have been developed
which enable us to get algebraic and geometric information about
the entire solution space of system (1). They are based on the
Gröbner
bases theory worked out by B.Buchberger around the middle of 60th of
last century. The idea of the methods is to find the "best"
representation of the corresponding variety.
To illustrate this recall that the Gauss-Jordan elimination
method transforms a system of linear equations into the so-called
row echelon form. The system thus obtained has exactly the same
solutions
(the variety) as the original system, but it is trivial to solve.
The other example is the system (1) with
is the field of real or complex numbers).
In algebraic geometry the solution space of system (1) is called
the variety. There are many numerical algorithms for solving
non-linear systems such as (1). These algorithms solve for one solution
at a time, and find an approximation to the solution.
They ignore the geometric properties of the solutions space (the
variety),
and do not take into consideration possible alternate descriptions of
the variety (using a different system of polynomials).
However recently efficient computational algorithms have been developed
which enable us to get algebraic and geometric information about
the entire solution space of system (1). They are based on the
Gröbner
bases theory worked out by B.Buchberger around the middle of 60th of
last century. The idea of the methods is to find the "best"
representation of the corresponding variety.
To illustrate this recall that the Gauss-Jordan elimination
method transforms a system of linear equations into the so-called
row echelon form. The system thus obtained has exactly the same
solutions
(the variety) as the original system, but it is trivial to solve.
The other example is the system (1) with 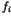 being
polynomials in a single variable,
being
polynomials in a single variable,
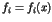 . In this case there is a polynomial
. In this case there is a polynomial 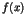 such that the system (1) is equivalent to the equation
such that the system (1) is equivalent to the equation
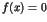 . The polynomial
. The polynomial 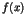 is the greatest common divisor of
is the greatest common divisor of
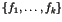 and it can be found using the Euclidean Algorithm.
Although the Gauss-Jordan elimination method cannot be directly
expanded to the case of non-linear polynomials and the Euclidean
Algorithm - to the case of
multivariable polynomials, it turns out that
an expansions of
these methods is possible, and, in a sense, the Gröbner bases theory
is a generalization of the Gauss-Jordan method and the Euclidean
Algorithm
to the case of non-linear multivariable polynomials.
and it can be found using the Euclidean Algorithm.
Although the Gauss-Jordan elimination method cannot be directly
expanded to the case of non-linear polynomials and the Euclidean
Algorithm - to the case of
multivariable polynomials, it turns out that
an expansions of
these methods is possible, and, in a sense, the Gröbner bases theory
is a generalization of the Gauss-Jordan method and the Euclidean
Algorithm
to the case of non-linear multivariable polynomials.
In the lecture we give an introduction to the Gröbner bases theory,
discuss some algorithms implemented in computer algebra systems
(e.g. in Mathematica) and consider a few applications to the theory of
dynamics systems, in particular, to the investigation of the
time-reversible systems of ODE.
References
Adams W W and Loustaunau P 1994 An Introduction to Gröbner
bases. Graduate Studies in Mathematics.-V.3. RI:AMS.
Becker T and Weispfenning V 1993
Gröbner Bases: A computational Approach to Commutative Algebra.
Graduate Texts in Mathematics, V.141. Berlin and New York: Springer-Verlag.
Buchberger B 1985 in
Multidimensional Systems Theory, ed. N.K.Boese.
D.Reidel Pub. Co., 184-232.
Cox D, Little J, O'Shea D 1992 Ideals, Varieties,
and Algorithms. New York: Springer-Verlag.
Jarrah, A, Laubenbacher, R and Romanovski V 2001 The center variety of
polynomial differential systems, preprint,
http://xxx.lanl.gov/abs/math.DS/0009061



Next: Rosenblum
Up: Abstracts
Previous: Robnik