


Next: Grossmann
Up: Abstracts
Previous: Gaspard
Experimental modeling of chaotic fields
Igor Grabec
Faculty of Mechanical Engineering
University of Ljubljana, Ljubljana, Slovenia
Physical description of natural laws is based on evolution equations
of fields but their analytical formulation is often not possible for
very complex chaotic phenomena [1]. In the lecture we show how a
method of chaotic time series prediction can be generalized to
statistical modeling of chaotic fields [2, 3]. For this purpose we
assume that a record of the field is provided by an experiment and
that the field amplitude 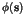 at a point of observation
at a point of observation
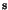 is related to amplitudes in a surrounding region. We
represent the field values in the surrounding region by the vector
is related to amplitudes in a surrounding region. We
represent the field values in the surrounding region by the vector
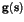 , and describe the field evolution by the mapping
equation
, and describe the field evolution by the mapping
equation

in which the function 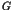 is estimated statistically. For this purpose
is estimated statistically. For this purpose
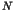 samples of the joint state vector
samples of the joint state vector
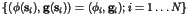 are first extracted from the
given record. As an optimal non-parametric estimator of the field at
point
are first extracted from the
given record. As an optimal non-parametric estimator of the field at
point 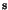 we employ the conditional average, which is expressed
by
we employ the conditional average, which is expressed
by
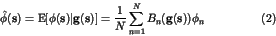
Here
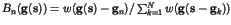 describes a similarity between the
given vector
describes a similarity between the
given vector
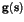 and a sample
and a sample 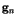 , while
, while 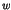 denotes a kernel function, such as Gaussian. The vector
denotes a kernel function, such as Gaussian. The vector
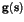 is considered as a given condition and is comprised from field
values in the surrounding of point
is considered as a given condition and is comprised from field
values in the surrounding of point 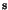 . During the calculation
of the conditional average the surrounding can be arbitrary selected,
which is an advantage of non-parametric estimator. To calculate a
field distribution in some domain, the field must be first specified
in a sub-domain. From given values the field distribution in the
surrounding of sub-domain can be estimated by Eq.2. The estimated
values are then considered as given ones and the procedure of field
estimation is iteratively continued. In the lecture optimal
statistical methods for selection of surrounding region of a point
. During the calculation
of the conditional average the surrounding can be arbitrary selected,
which is an advantage of non-parametric estimator. To calculate a
field distribution in some domain, the field must be first specified
in a sub-domain. From given values the field distribution in the
surrounding of sub-domain can be estimated by Eq.2. The estimated
values are then considered as given ones and the procedure of field
estimation is iteratively continued. In the lecture optimal
statistical methods for selection of surrounding region of a point
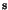 and self-organized determination of number
and self-organized determination of number 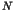 are
explained. Various examples of estimated chaotic filed distributions,
such as profiles of a rough surface [3, 4], charge density and
electron temperature in turbulent ionization waves in plasma, etc, are
demonstrated. The performance of the proposed statistical modeling is
described by comparing correlation functions and spectra of
experimentally recorded and estimated fields.
are
explained. Various examples of estimated chaotic filed distributions,
such as profiles of a rough surface [3, 4], charge density and
electron temperature in turbulent ionization waves in plasma, etc, are
demonstrated. The performance of the proposed statistical modeling is
described by comparing correlation functions and spectra of
experimentally recorded and estimated fields.
References
[1] Grabec I, 1986, Phys. Lett., A117(8), pp 384-386
[2] Grabec I, Sachse W, 1997, Synergetics of Measurement, Prediction and Control, (Springer-Verlag, Heidelberg)
[3] Grabec I, Mandelj S, 1997, Proc. Int. Conf. EANN'97 - Stockholm, Eds.: A. B. Bulsari, S. Kallio, (Åbo Akademis Tryckery, Turku, Finland), pp 357-360
[4] Mandelj S, Grabec I, Govekar E, 2000, CIRP J. of Manuf. Systems, 30(3), pp 281-287



Next: Grossmann
Up: Abstracts
Previous: Gaspard
![]() at a point of observation
at a point of observation
![]() is related to amplitudes in a surrounding region. We
represent the field values in the surrounding region by the vector
is related to amplitudes in a surrounding region. We
represent the field values in the surrounding region by the vector
![]() , and describe the field evolution by the mapping
equation
, and describe the field evolution by the mapping
equation