
Hotel PIRAMIDA, Maribor, Slovenia, 2 - 6 July 2007
Center for Applied Mathematics and Theoretical Physics
CAMTP, University of Maribor, Slovenia

|
8th JAPAN - SLOVENIA SEMINAR ON NONLINEAR SCIENCE Hotel PIRAMIDA, Maribor, Slovenia, 2 - 6 July 2007 Center for Applied Mathematics and Theoretical Physics |
References and Literature for Further Reading
[1] Y. Aizawa, Adv. Chem. Phys. 130B (2005) 465.
[2] T. Akimoto and Y. Aizawa, Nonlinear Phenom. Compl. Sys. 6 (2006) 178.
[3] S. Shinkai and Y. Aizawa, Prog. Theor. Phys. 116 (2006) 503.
[4] T. Akimoto and Y. Aizawa, J. Korean. Phys. Soc. 50 (2007) 254.
To examine an effect of non-equilibrium steady state (NESS) on phase transition, we analyze one-dimensional conductor which shows Peierls transition. Our system is connected to two heat baths which have different temperatures and chemical potentials, and is described by the following Hamiltonian:
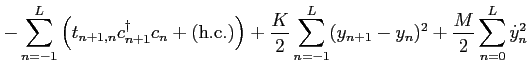 |
|||
 |
References and Literature for Further Reading
[1]
F. Sawano, I. Terasaki, H. Mori, T. Mori, M. Watanabe, N. Ikeda,
Y. Nogami and Y. Noda, Nature 437 (2005) 522.
Limit theorems for the time average of some observation functions in
the dynamical systems are studied. It is known that
intermittent phenomena, such as the Rayleigh-Benard convection and
Belousov-Zhabotinsky reaction, are described by non-hyperbolic
dynamical systems, and the invariant measure of such dynamical systems
can not be normalized (infinite measure).
We show that the time average of some observation functions
converges in some distributions which depend on the properties of observation
functions and whether the invariant measure is finite or not.
In the case of the infinite measure, the time average
converges to the generalized arcsine distribution
when the observation function is not the ![]() function, whose average
with respect to the invariant measure
function, whose average
with respect to the invariant measure ![]() is finite.
This result gives new points that
the correlation function defined by the time average:
is finite.
This result gives new points that
the correlation function defined by the time average:
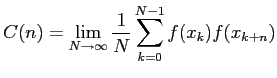
does not decay and converges in distribution for all
References and Literature for Further Reading
[1]G. D. Birkhoff, Proc. Nat. Acad. Sci. USA,
17 (1931), 656-660.
[2]D. A. Darling and M. Kac, Trans. Amer. Math. Soc., 84 (1957), 444-458.
[3] J. Aaronson, An Introduction to Infinite Ergodic Theory,
American Mathematical Society, (1997)
[4] M. Thaler, Trans. Amer. Math. Soc., 350 (1998), 4593-4607.
[5] M. Thaler and R. Zweim
![]() ller, Probab. Theory Relat. Fields, 135 (2006), 15-52.
ller, Probab. Theory Relat. Fields, 135 (2006), 15-52.
[6] J. Lamperti, Trans. Amer. Math. Soc., 88 (1958), 380-387.
[7] T. Akimoto and Y. Aizawa, Nonlinear Phenomena in Complex Systems, 6 (2006), 178-182.
[8] T. Akimoto and Y. Aizawa,
Journal of the Korean Physical Society, 50 (2007), 254-260.
We consider an AB ring consisting of two magnetic impurities with
the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction and Kondo effect.
These two interactions compete with each other.
In recent experiments [4], this competition was observed.
We will show how the interference effects induce the anisotropic RKKY interaction [5].
We also report spin conductance as well as charge conductance
using the slave boson mean field approximation.
References and Literature for Further Reading
[1] Y. Aharonov and A. Casher,
Phys. Rev. Lett. 53, 319 (1984).
[2] J. Nitta, F. E. Meijer, and H. Takayanagi,
Appl. Phys. Lett. 75, 695 (1999).
[3] M. König et al.,
Phys. Rev. Lett. 96, 076804 (2006).
[4] N. J. Craig et al.,
Science 304, 565 (2004); H. B. Heersche 促etal,
Phys. Rev. Lett. 96, 017205 (2006).
[5] T. Aono, cond-mat/0608587.
Non-parametric statistical modeling is a powerful tool for predicting evolution of deterministic chaotic fields. It is based on assumption that statistical properties of deterministic chaotic fields remain unchanged as the field evolves with time. An analysis of field patterns in the past enables us to extract relations between values of field in neighboring points in space as well as in time. Based on similarities between the present field pattern and field patterns extracted from the past data, the field value in the next time step can be successfully predicted.
In my presentation a special attention will be paid to the optimization of field pattern sampling. It will be
shown how to sample a set of patterns, which gives the highest quality field prediction. The proposed
method will be illustrated on two examples, an analytical model of chaotic discrete coupled map lattice
and an experimentally obtained record of surface optical activity in laser welding process.
References and Literature for Further Reading
[1] A. Borštnik Bračič, E. Govekar, I. Grabec,
DCDIS A Supplement, Advances in Neural Networks 14 (S1) (2007) 227-231.
[2] I. Grabec, European Physical Journal B
48 No. 2 (2005) 279-289.
[3] S. Mandelj, I. Grabec, E. Govekar,
International Journal of Bifurcation and Chaos 14 No.6 (2004) 2011-2025.
[4] I. Grabec, S. Mandelj,
Progress of Theoretical Physics Supplement 150 (2003) 81-88.
[5] E. Govekar, J. Gradišek, I. Grabec, M. Geisel, A. Otto, M. Geiger,
"On characterization of CO![]() laser welding process by means of light emitted
by plasma and images weld pool", in Third Int.
Symp: Investigation of Non-linear Dynamics Effects in Production Systems
(Cottbus, Germany) (2000).
laser welding process by means of light emitted
by plasma and images weld pool", in Third Int.
Symp: Investigation of Non-linear Dynamics Effects in Production Systems
(Cottbus, Germany) (2000).
Aging is not a phenomenon restricted to us humans. Here presented is a
theory of aging in globally and diffusively coupled oscillators.
We introduce "aging" in such a way that a finite fraction (say ![]() ) of
oscillators is "inactive", meaning a damped oscillator in a generalized
sense including overdamped cases. We then show analytically as well as
numerically that if the coupling strength
) of
oscillators is "inactive", meaning a damped oscillator in a generalized
sense including overdamped cases. We then show analytically as well as
numerically that if the coupling strength ![]() is
larger than a threshold value, the whole system stops oscillation at a
less than one value of
is
larger than a threshold value, the whole system stops oscillation at a
less than one value of ![]() . This is what we call an aging transition,
whose universal aspects will be uncovered.
Moreover, under certain conditions, the group of "active" oscillators(i.e.
self-sustained oscillators) is shown
to split into clusters in a horn-shaped region of the
. This is what we call an aging transition,
whose universal aspects will be uncovered.
Moreover, under certain conditions, the group of "active" oscillators(i.e.
self-sustained oscillators) is shown
to split into clusters in a horn-shaped region of the ![]() phase diagram.
Bifurcations and clustering dynamics therein will be discussed in detail
by confining ourselves to a simplest category of clustering.
This clustering phenomenon provides a new type of diffusion-induced inhomogeneity
in nonlinear dynamics, whose mechanism will also be discussed. (A full list
of references is given in [5] below.)
phase diagram.
Bifurcations and clustering dynamics therein will be discussed in detail
by confining ourselves to a simplest category of clustering.
This clustering phenomenon provides a new type of diffusion-induced inhomogeneity
in nonlinear dynamics, whose mechanism will also be discussed. (A full list
of references is given in [5] below.)
References and Literature for Further Reading
[1] H. Daido and K. Nakanishi, Phys. Rev. Lett. 93
(2004) 104101.
[2] K. Nakanishi and H. Daido, Prog. Theor. Phys. Suppl. 161 (2006) 173.
[3] H. Daido, Nonliner Phenomena in Complex Systems,
in the press.
[4] H. Daido and K. Nakanishi, Phys. Rev. Lett. 96 (2006)
054101.
[5] H. Daido and K. Nakanishi, Phys. Rev. E 75 (2007)
056206.
Recently an extrasolar system was discovered, where the observers predicted
that there exists a terrestrial planet in a habitable zone around the star
Gliese 581. We will discuss the dynamical stability of this system, but also
the possibility of earthlike planets in other extrasolar systems in such zones
where water could be found in a liquid form.
References and Literature for Further Reading
[1] R.Dvorak, F.Freistetter, in Lecture Notes in Physics: Chaos and Stability in Planetary Systems 683 (2005) 3-136.
[2] J. Schneider: The Extrasolar Planets Encyclopaedia, http://exoplanet/eu
The large deviation statistics is an extension of the central limit theorem
and has a close connection with the equilibrium statistical mechanics,
the multi-fractal theory of turbulence and chaos.
The large deviation statistical functions are determined by the
largest eigenvalue of the operator ![]() defined by
defined by
for the differential equation systems (chaotic or stochastic) and
for the discrete time dynamics such as chaotic maps and finite state Markoffian processes. Here
References and Literature for Further Reading
[1] H. Fujisaka and M. Inoue, Prog. Theor. Phys. 77
(1987) 1334.
[2] H. Fujisaka and M. Inoue, Phys. Rev. A 39
(1989) 1376.
[3] H. Fujisaka and T. Yamada, Phys. Rev. E 75 (2007) 031116.
We study the spatio-temporal dynamics of an
anisotropic ![]() system driven by circularly polarized external field using the Ginzburg-Landau model
system driven by circularly polarized external field using the Ginzburg-Landau model
| (1) |
We observe a variety of spatio-temporal structures depending on the
symmetry of the uniform oscillation.
In the case that two stable uniform limit cycles coexist, we observe the domain wall which connects two different limit cycles. The domain walls temporally oscillate in the presence of the periodic external field. Due to the symmetry of the model, there are two types of domain wall structures, Néel
wall and Bloch wall.
In the case that the uniform solution shows the quasiperiodic
oscillation, propagation of the phase wave is observed.
Our result suggests that phase dynamics can be applicable even in
nonautonomous systems.
Moreover, we find spatio-temporal chaos in some parameter range.
In this presentation,
dynamical characteristics of these patterns are reported.
A technique to stabilize the unstable Néel wall is
also discussed.
References and Literature for Further Reading
[1] N. Fujiwara, T. Kobayashi, and H. Fujisaka,
Phys. Rev. E 75
(2007) 026202.
[2] N. Fujiwara, H. Tutu, and H. Fujisaka,
Phys. Rev. E 70 (2004) 066132.
[3] B. K. Chakrabarti and M. Acharyya,
Rev. Mod. Phys. 71 (1999) 847.
Development of an automatic information processing system capable of statistical modeling of physical laws is treated. The system is comprised of an array of sensors and a network of memory cells called artificial neural network (ANN). As the primary object of modeling the joint probability density function (PDF) of signals from sensors is considered. It is expressed by a kernel estimator based upon discrete samples of data. Since the number of samples can increase without limit, while the number of memory cells is generally limited, the problem arises how to proceed to an optimal representation of sensory data and proper storage in the memory cells. To solve this problem a new principle of absolute maximum entropy is formulated and applied to express a representative PDF in terms of prototype data. The modeling of a specific physical law is performed by a mapping of sensory signals to these prototype data. For this purpose the discrepancy between the PDF of sensory data and the representative one is minimized. The adaptation process leads to a self-organized, highly non-linear dynamics of memory cells in an abstract multi-dimensional space. The dynamics is non-autonomous since it is driven by sensory data. The corresponding algorithm includes two steps that correspond to initialization and adaptation of prototype data. Its stochastic perturbation treatment leads to an adaptation process that resembles the cooperation of neurons in biological neural networks. During adaptation each neuron is selectively sensitized to one prototype from the sample space of the driving variable. The response of the complete network is described by the excitation of neurons which causes self-organization and simultaneously represents the encoded driving variable. During adaptation each neuron is selectively sensitized to one prototype from the sample space of the driving variable. The response of the complete network is described by the excitation of neurons which causes self-organization and simultaneously represents the encoded driving variable. The corresponding self-organization of neurons has been previously described by Kohonen based upon biological observations. In the presentation the self-organized formation of neurons in an ANN is demonstrated on one-and two-dimensional examples of sensory data.
As the secondary object of modeling an optimal extraction of relations between signals from various sensors is considered. For this purpose the conditional average is proposed as an optimal estimator. It is simply expressed in terms of prototype data and represents a general, non-linear and non-parametric regression that is widely applicable in various fields of automatic statistical modeling of natural laws. Applicability of conditional average estimator is demonstrated on examples from physics, technology, and economy.
References and Literature for Further Reading
[1] I. Grabec, W. Sachse Synergetics of Measurements, Prediction and Control, Springer-Verlag, Berlin (1997).
[2] I. Grabec, Eur. Phys. J. B, 48 (2005) 279-289.
[3] B. Lunar Peček, I. Grabec, Neural Network World 12/3 (2002) 241-254.
[4] I. Grabec, S. Mandelj, Progress in Theoretical Physics, Suppl.150 (2003) 81-88.
Various kinds of devices such as lasers and musical instruments utilize stationary wave oscillations in resonant cavities. In order to maintain the stationary oscillation in these devices, nonlinearity is essential in the mechanism for balancing the pumping of the external energy and the decay of the wave of the quasi-stable resonance in the resonant cavity. Besides, the interaction between nonlinearities and the morphology of the boundary condition imposed on a resonating wave system by the shape of the cavity is also very important for determining the modes of oscillation.
1D simple shapes have been used for laser cavities because they are suitable for fabrication as well as application of directional emission. However, recent advances in processing technology of dry-etching for semiconductor laser diodes have made it possible to fabricate 2D microcavity lasers of arbirary 2D shapes with potential applications of 2D emission of laser light in optical communications and optical integrated circuits.
We will review the theoretical models of 2D microcavity lasers
and discuss their applications.
References and Literature for Further Reading
[1] Chang R K and Campillo A J, eds.: Optical processes in microcavities (World Scientific Publishing, Singapore, New Jersey, Hong Kong, 1996).
[2] Nöckel J U and Stone A D, Nature 385 45, 1997.
[3] Gmachl C, Capasso F, Narimanov E E, Nöckel J U, Stone A D, Faist J, Sivco D L, and Cho A Y, Science 280 1556, 1998.
[4] Harayama T, Davis P, and Ikeda K S, Phys. Rev. Lett. 82 3803, 1999.
[5] Harayama T, Davis P, and Ikeda K S , Phys. Rev. Lett. 90 063901, 2003.
[6] Harayama T, Fukushima T, Sunada S and Ikeda K S , Phys. Rev. Lett. 91 073903, 2003.
[7] Fukushima T and Harayama T, IEEE J. Select. Topics Quantum Electron. 10 1039, 2006.
[8] T. Harayama and S. Sunada, To be published in Phys. Rev. E, 2007.
[9] Susumu Shinohara and Takahisa Harayama, Phys. Rev. E 75, 036216-1-4, 2007.
[10] T. Tanaka, M. Hentschel, T. Fukushima, and T. Harayama, Phys. Rev. Lett.98, 033902, 2007.
[11] S. Shinohara, T. Harayama, H. Tureci, and A. D. Stone, Phys. Rev. A74, 033820-1-5, 2006.
[12] S. Sunada and T. Harayama, Phys. Rev. A 74, 021801-1-4, 2006.
[13] M. Choi, T. Tanaka, T. Fukushima, and T. Harayama, Appl. Phys. Lett.88, 211110-1-3, 2006
[14] T. Fukushima, T. Harayama, and J. Wiersig, Phys. Rev. A73, 023816-1-4, 2006
[15] T. Harayama, S. Sunada, and K. S. Ikeda, Phys. Rev. A72, 013803-1-12, 2005.
[16] T. Fukushima, T. Tanaka, and T. Harayama, Appl. Phys. Lett.87, 191103-1-3, 2005.
[17] S. Sunada, T. Harayama, and K.S. Ikeda, Phys. Rev. E71, 046209-1-5, 2005.
[18] T. Fukushima, T. Tanaka, and T. Harayama, Appl. Phys. Lett.86, 171103-1-3, 2005.
In order to reveal whether the spring-block model is useful with respect to a reproduction of the seismicity in nature, we analyze statistical properties produced by a two-dimensional model involving stick-slip behavior. We find that the model reproduces spatio-temporal interval statistics semi-quantitatively, in addition to the Gutenberg-Richter (GR) law and the power-law size distribution, in a restricted parameter regime. At this regime, the model yields a realistic b-value of the GR law and ratio of seismic wave velocity, and shows a statistical property of the stress distribution, the constant stress drop. The critical state of the system is evaluated from statistical properties we focus on. The results are summarized by means of a phase diagram. We conclude that the spring-block model exhibits a state of the self-organized criticality when the model adequately reproduces the seismicity in nature.
References and Literature for Further Reading
[1] J. M. Carlson and J. S. Langer, Phys. Rev. A 40
(1989) 6470.
[2] P. Bak, C. Tang and K. Wiesenfeld, Phys. Rev. A 38 (1988) 364.
[3] P. Bak and C. Tang, J. Geophys. Res. 94 (1988) 15635.
[4] T. Mori and H. Kawamura, J. Geophys. Res. 111
(2006) B07302.
[5] H. Kumagai, Y. Fukao, S. Watanabe, and Y. Baba, Geophys. Res .Lett. 26 (1999) 2817.
[6] T. Hasumi, submitted.
The quantum-classical correspondence (QCC) is the basic principle underlying any physical quantisation of a classical system. According to this principle the quantum system should behave similar to the corresponding classical system with increasing energy or decreasing effective Planck constant.
We investigate time evolution of QCC in fully chaotic maps on a torus [1] with the periodic boundary conditions. The quality of the QCC is measured by the quantum-classical fidelity (QCF)[2], which is an overlap of the classical phase-space density and the corresponding Wigner function of the quantum system .
Numerically and by heuristic arguments we found that in the generic chaotic systems QCF stays at initial value up to an Ehrenfest-type time scale and after that it decays exponentially with the rate given by the maximal Lyapunov exponent to some ergodic plateau. In systems with the Egorov property [3] e.g. Arnold's cat map, which roughly means that classical and quantum time evolution commute, the QCF can stay at the initial value almost arbitrarily long and then decays faster than exponentially.
References and Literature for Further Reading
[1]Degli Esposti M and Graffi S 2003
The mathematical aspects of quantum maps, Lecture Notes in Physics, volume 618
(Springer-Verlag)
[2] Horvat M, Prosen T and Degli Esposti M 2006
Quantum-classical correspondence on compact phase space
Nonlinearity 19 1-23
[3] Horvat M and Degli Esposti M 2007
Egorov property in perturbed cat map
submitted to J. Phys. A: Math. Theo.
Transmembrane proteins have long been considered to be critical in understanding biological functions such as cell signaling, ion transport, and intercellular communication. It has been reported that approximately 45% of the drugs in use today target G protein-coupled receptors (GPCRs). Some 20% to 30% of genes in an average genome are estimated to encode membrane proteins. Because of their biological and pharmaceutical importance, identification of transmembrane helices in membrane proteins is a priority. Although promising methods in X-ray crystallography and nuclear magnetic resonance (NMR) have begun to open avenues to the determination of these structures, the number of known three-dimensional structures remains small. Therefore, reliable algorithms to predict transmembrane protein structures would be very useful.
An approch utilizing a finite-state, stochastic dynamical system (Hidden Markov Model (HMM)) has been successful in creating algorithms for predicting transmembrane protein secondary structure.
Here, we present an algorithm for predicting transmembrane secondary structures using two-dimensional vector trajectories consisting of a hydropathy index and formal charge of an amino acid sequence using stochastic dynamical system models.
The prediction accuracies, using a collection of publicly available transmembrane protein sequences, suggest that stochastic dynamical system models perform reasonably well on bilogical data as well.
References and Literature for Further Reading
[1] T. Kaburagi, D. Muramatsu, and T. Matsumoto, J. Bioinformatics and Computational Biology 5(3) (2007) (in press).
[2] A. Krogh, B. Larsson, G. von Heijne, and E. L. L. Sonnhammer,, J. Molecular Biology 305(3) (2001) pp. 567-580.
[3] G. E. Tusnady and I. Simon, J. Molecular Biology 283(2) (1998) pp. 489-506 .
[4] T. Hirokawa, S. Boon-Chieng, and S. Mitaku, Bioinformatics 14(4) (1998) pp. 378-379
[5] C. P. Chen and B. Rost, Appl. Bioinformatics 1(1) (2002) pp. 21-35
Research of structure, dynamics and macroscopic properties of complex systems
has grown fast over recent years. Colloids, biopolymers, biological cells,
porous matter and other complex heterogeneous materials are considered as complex
systems in condensed matter physics. The relaxation phenomena and kinetics in
such systems cannot be described by Debye type response function and Brownian
diffusion as a rule. We consider dielectric spectra of two systems: clay-water
mixtures and cement pastes. The measured dielectric responses are described by
considering the microscopic ion dynamics. We treat the motion of the
classical particle in the fluid interrupted by trapping events and show that
the anomalous features of the dielectric spectra can be reproduced by choosing
the long-tailed waiting time probability density function of the trapping events.
The possible correlations between the structure of the complex system and the
dynamics are indicated.
References and Literature for Further Reading
[1] R. Metzler and J. Klafter, Phys. Rev. E 61 (2000) 6308-6311.
[2] Y. Feldman, A. Puzenko, Y. Ryabov, Chem. Phys. 284
(2002) 139-168.
[3] H. Sanabria and J. H. Miller, Phys. Rev. E 74 (2006) 051505.
[4] B. Rotenberg, A. Cadene, J. -F. Dufreche, S. Durand-Vidal, J. -C.
Badot, and P. Turq, J. Phys. Chem. B 109 (2005) 15548-15557.
[5] W. T. Coffey, Yu. P. Kalmykov, J. T. Waldron,
The Langevin Equation Singapore, World Scientific (2004).
[6] C. W. Gardiner, Handbook of Stochastic Methods 3rd ed. Berlin,
Springer (2004).
[7] L. D. Landau, E. M. Lifshitz and L. P. Pitaevskii,
Electrodynamics of Continuous Media 2nd ed., Oxford, Butterworth-Heineman
(1993).
Domain patterns are observed in various physical and chemical systems:
for example, thermal convection in fluids, chemical reaction systems,
ferromagnetic thin films, ferrofluids, etc [1,2].
In this talk, we focus on magnetic domain patterns in a ferromagnetic
thin film. Magnetic domain patterns after quench show various type of
patterns depending on the field sweep rate and parameters of the model
[3,4].
We will show how the domain patterns are formed under decreasing field
with use of the number of domains and the domain area as well as
snapshots of domain patterns simulated with a simple Ising-like model.
We will also propose a criterion about the field sweep rate and the
structure of domain patterns. Under oscillating field, magnetic domain
patterns can display more interesting structures.
Some patterns travelling very slowly compared with the time scale
of the field are observed under some conditions.
We will show some simulated travelling magnetic patterns and propose
two analytical ways to investigate the effects of the oscillating field
[5].
References and Literature for Further Reading
[1] M. C. Cross and P. C. Hohenberg, Rev. Mod. Phys.
65 (1993) 851.
[2] M. Seul and D. Andelman, Science 267 (1995) 476.
[3] K. Kudo, M. Mino and K. Nakamura, J. Phys. Soc. Jpn
76 (2007) 013002.
[4] K. Kudo and K. Nakamura, arXiv:cond-mat/0702126 (2007).
[5] K. Kudo and K. Nakamura, arXiv:0704.3870 (2007).
In biological cells calcium enables reliable and effective signal transduction connecting extracellular signals with intracellular functions. The question arises how only one intermediate (calcium) is able to connect different input signals with different cellular processes, which is known as the bow-tie or hour-glass architecture of cellular signalling [1].
We propose mathematical models for the key cellular mechanisms enabling simultaneous transmission of different signals. The first model exploits the complexity of calcium signals. In particular, for bursting oscillations we show the possibility of selective regulation of different cellular processes [2]. In the second model we show that a two-level protein cascade can act as a band-pass filter for time-limited calcium oscillations. These band-pass filters can further be combined into a network of three-level signalling cascades that by filtering the frequency of time-limited oscillations selectively switches cellular processes on and off [3]. For special conditions, we were able to develop a minimal model for band-pass filtering of time-limited calcium oscillations [4].
The problem of simultaneous signal transmission is much more general and our models are compared with known mechanisms in technical systems. We found relations with multiplexers in communication systems. Examples of such common procedures are code-division multiple access (CDMA) and time-division multiplexing (TDMA) used by the GSM telephone system, for example.
References and Literature for Further Reading
[1] M. Csete, J. Doyle, Trends Biotechnol. 22 (2004) 446-450.
[2] S. Schuster, B. Knoke, M. Marhl, BioSystems 81 (2005) 49-63.
[3] M. Marhl, M. Perc, S. Schuster, FEBS Lett. 579 (2005) 5461-5465.
[4] M. Marhl, M. Perc, S. Schuster, Biophys. Chem. 120 (2006) 161-167
References and Literature for Further Reading
[1] S. Masuda and K. Nakamura, J. Phys. Condens. Matter. 19
(2007) 216225
~syuji/
Chaotic piecewise linear map whose statistical properties are identical to
those of a random walk on directed graphs such as the world wide web (WWW)
is constructed, and the dynamic quantity is analyzed in the framework of
large deviation statistics. Gibbs measures include the weight factor
appearing in the weighted average of the dynamic quantity,
which can also quantitatively measure the importance of web sites.
Currently used levels of importance in the commercial search engines are
independent of search terms, which correspond to the stationary visiting frequency
of each node obtained from a random walk on the network
or equivalent chaotic dynamics.
Levels of importance based on the Gibbs measure depend on each search term
which is specified by the searcher.
Also is discussed topological conjugate transformation between one dynamical system with a Gibbs measure
and another dynamical system whose standard invariant probability measure is identical to the Gibbs measure.
References and Literature for Further Reading
[1] Syuji Miyazaki, Springer LNAI series 4012 "New Frontiers in Artificial Intelligence: Proceeding of the 19th Annual Conferences of the Japanese Society for Artificial Intelligence"
(2006) 261-270.
[2] Syuji Miyazaki, Progress of Theoretical Physics Supplement 162 (2006) 147-154.
[3] Syuji Miyazaki, Springer new series "Studies in Computational Intelligence" volume 56,
(2007) 129-137.
In this context we revisit the Kramers theory as an eigenvalue problem
of the Fokker-Planck operator.
Firstly, we explore the relaxation process in a triple-well symmetric Landau potential by the WKB analysis.
We will report a formula which is a subtle extension to the
so-called Kramers escape rate in the case of the structured potential,
where the activation energy is effectively lowered compared to
the case of a single parabolic barrier.
Secondly, a nonequilibrium extension of the formula
will be explored for the tilted double-humped periodic potential
by assuming the complex eigenvalues of the FP operator.
References and Literature for Further Reading
[1] O.Galkin, and P.G.Vekilov, Journal of Crystal Growth 232 (2001) 63.
[2] Takaaki Monnai, Ayumu Sugita, and Katsuhiro Nakamura, Phys.Rev.E 74 (2006) 061116.
[3] Takaaki Monnai, Ayumu Sugita, and Katsuhiro Nakamura, submitted to Phys.Rev.E
[4] Takaaki Monnai, Ayumu Sugita, J.Hirashima, and Katsuhiro Nakamura, Physica D 219 (2006) 177
Bose-Einstein condensate(BEC) provides a nice playground where the nonlinear Schrödinger equation plays a vital role (see Reference below). We study the dynamics of multi-component BEC in 2 dimensions with and without harmonic traps by using the nonlinear Schrödinger (or Gross-Pitaevskii) equation.
Firstly we consider a driven two-component BEC with each component trapped in different vertical positions. The appropriate tuning of the oscillation frequency of the magnetic field (Franck-Condon transition) leads to a striking anti-gravity transport of BEC. This phenomenon is a manifestation of macroscopic non-adiabatic tunneling in a system with two internal(electronic) degrees of freedom.
Secondly, we examine the three-component repulsive BEC in 2 dimensions in a harmonic trap in the absence of magnetic field, and construct a model of conservative chaos based on a picture of vortex molecules. We obtain an effective nonlinear dynamics. The vortices here acquire the inertia in marked contrast to the standard theory of point vortices since Onsager. We then explore "the chaos in the three-body problem" in the context of vortices with inertia.
Finally we analyze the billiard motions of 2-d solitons, showing a variety of collisions among solitons and the collision with hard walls. The resultant features are astonishingly different from the well-known diffusion and interference of wave packets in the dynamics based on the linear quantum mechanics.
This work owes to my collaborators, V. M. Pérez-Garcıa, V. V. Konotop, D. Matrasulov,
M. Kobayashi and A. Kohi. The full details will be published elsewhere.
References and Literature for Further Reading
[1] K. Nakamura,Prog. Theor. Phys. Suppl. (Kyoto) 166 (2007), in press.
The dynamics of traveling waves in a nonlinear dissipative system are
studied analytically and numerically. Spatio-temporal forcing and feedback
forcing are applied to the traveling waves in a phase-separated system
undergoing chemical reactions. The stability of the traveling waves and
interesting, unexpected
behavior, including the trapped coherent oscillations of the waves and the
reversal of the propagation direction are analyzed in one dimension. The
phase dynamical approach is applied to gain a theoretical understanding of
the dynamics.
References and Literature for Further Reading
[1] A. Pikovsky, M. Rosenblum and J. Kurths,
Synchronization: A universal concept in nonlinear sciences, New York,
Cambridge university press (2001).
[2] E. Schöll,
Nonlinear spatio-temporal dynamics and chaos in semiconductors, New
York, Cambridge university press (2001).
[3] T. Ohta and H. Tokuda, Phys. Rev. E 72
(2005) 046216.
[4] H. Tokuda and T. Ohta, J. Phys. Soc. Jpn 75 (2006)
064005.
[5] H. Tokuda, V. Zykov and T. Ohta, Phys. Rev. E in press.
Evolutionary game theory is currently undergoing quite a renaissance in view of possible interrelations with topics of physics. Examples are studies of different phase transitions, coherence resonances, and complex network induced phenomena. The goal of my talk is to present a brief overview of recent results that appear to have far-reaching consequences and shed new light towards resolving the conflict underlying the evolution of cooperation in societies governed by egoistic Darwinian individuals.
References and Literature for Further Reading
[1] C. Hauert and G. Szabó, Am. J. Phys. 73 (2005) 405.
[2] G. Szabó and G. Fáth, arXiv:cond-mat 0612316.
[3] M. Perc, New J. Phys. 8 (2006) 22.
A signature of quantum chaos in quantum systems can be revealed
by comparison to the properties of random matrix ensembles.
We consider a quantum spin chain with nearest-neighbor
two-body random coupling, interacting with random external field.
Such a model has many interesting properties among which we find
particulary important the quantum phase transition
which occurs when the strength of external field vanishes.
A clear signature of criticality is provided by the gap
scaling with the system size where universal power-law dependence
is obtained for any non-zero field whereas in the critical case the decay is clearly faster.
Similarly, higher degree of entanglement of the ground state
in the absence of external field is manifested in slower decay of spatial long-range correlations.
The entanglement entropy for infinite chain is finite for all non-zero external fields but the limiting value gradually increases when the field is weakened and in the critical case the entanglement entropy
diverges logarithmically.
References and Literature for Further Reading
[1] F. Haake,
Quantum Signatures of Chaos - 2nd Ed., Berlin, Springer (2001).
[2] G. Vidal, J. I. Latorre, E. Rico, and A. Kitaev, Phys. Rev. Lett. 90 (2003) 227902.
We numerically investigate Heisenberg XXZ spin-![]() chain in a spatially random (disordered) static magnetic field [1]. We find that time dependent density matrix renomalization group simulations of time evolution of the model can be performed efficiently. Namely, the dimension of matrices needed to efficiently represent the time-evolution increases
linearly with time, or entanglement entropy of typical bipartition of the lattice grows logarithmically in time. This has to be contrasted with exponential inefficiency of classical simulations
of non-integrable spin chains in homogeneous fields [2].
chain in a spatially random (disordered) static magnetic field [1]. We find that time dependent density matrix renomalization group simulations of time evolution of the model can be performed efficiently. Namely, the dimension of matrices needed to efficiently represent the time-evolution increases
linearly with time, or entanglement entropy of typical bipartition of the lattice grows logarithmically in time. This has to be contrasted with exponential inefficiency of classical simulations
of non-integrable spin chains in homogeneous fields [2].
As a result, we have shown [1] that infinite temperature density-density correlation function of XXZ
model in the random field displays exponential localization in space indicating insulating behavior of the model. Similar results have been found for other examples of non-integrable spin chains with nearest neighbour interaction in external random fields.
References and Literature for Further Reading
[1] M. Žnidarič, T. Prosen and P. Prelovšek, Many-body pseudo-localization in Heisenberg XXZ magnet in a random field, preprint, to be submitted.
[2] T. Prosen and M. Žnidarič, Phys,. Rev. E 75 (2007) , 015202(R).
In order to celebrate mathematics in the new millennium, The Clay Mathematics Institute of Cambridge, Massachusetts has named seven Millennium Prize Problems. They selected these problems, focusing on important classic questions that have resisted solution over the years and they have designated a 7 million dollars prize fund for the solution to these problems, with 1 million dollars allocated to each. In this talk we shall look at the history of one of these problems - the Poincaré Conjecture, which has recently been solved in a spectacular way by Russian mathematician Grigorij Perel'man. We shall also list the key remaining open problems and related conjectures.
To get an idea about this famous problem, which has attracted attention of several leading mathematicians around the world, for almost a century, consider stretching a rubber band around the surface of an apple. Clearly, we can shrink it down to a point by moving it slowly, without tearing it and without allowing it to leave the surface. On the other hand, if we imagine that the same rubber band has somehow been stretched in the appropriate direction around a doughnut, then there is no way of shrinking it to a point without breaking either the rubber band or the doughnut.
We say the surface of the apple is "simply connected," but that the surface of the doughnut is not. Henri Poincaré, the famous French mathematician and the founder of topology, knew almost a hundred years ago that a two dimensional sphere is essentially characterized by this property of simple connectivity, and asked the corresponding question for the three dimensional sphere (the set of points in the four dimensional space at the unit distance from the origin). This question turned out to be extraordinarily difficult, and mathematicians have been struggling with it for decades, some even publishing wrong proofs and many more making false announcements - most of the proof, but some also of the counterexample.
We shall present the dramatic story from the last 3 years, which started with the announcement by Perel'man of the complete solution in a set of incomplete preprints, which he posted on the web, and the fight for priority which followed thereafter, mostly between China and United States. Last year two Chinese geometers hastily wrote and published (in total secrecy) a volumnious paper with even a more general proof (they claim the Thurston Geometrization Conjecture), only to be followed few weeks later by a very well-known geometer+topologist pair of authors from United States, who published an entire book with the details of Perel'man's proof.
The discussion may have reached US courts by now, as one of the key protagonists, a Chinese geometer, threatened with a legal suit against the magazine which published an unflattering (to him) story in the sequel to this stormy debate. The controversy got the attention around the world, since Perel'man refused to accept the greatest prize in mathematics, the Fields medal, which was to be presented to him in Madrid last summer by the King of Spain. Moreover, he quit his research post at the Sankt Petersburg Branch of the Steklov Mathematical Institute and has refused all contacts therafter. Of course, at present no one knows who, if anyone, will collect the one million dollars prize for the solution of this millenium problem.
References and Literature for Further Reading
[1] G. Besson, Séminaire Bourbaki. Astérisque. 307 (2006), 309-347.
[2] H.-D. Cao, X-P. Zhu, Asian J. Math. 10 (2006), 165-492.
[3] J. W. Morgan, Bull. Amer. Math. Soc. 42 (2005), 57-78.
[4] J. W. Milnor, Clay Math. Inst., Cambridge, MA. (2006), 71-83.
[5] D. Repovš, Geometric and Algebraic Topology. PWN, Warsaw (1986), 77-108.
[6] D. Repovš, Kodai Math. J. 17 (1994), 538-548.
[7] R. J. Daverman, D. Repovš, Trans. Amer. Math. Soc. 315 (1989), 219-230.
We treat real 2D matrices and calculate the level spacing distribution
![]() for a number of different random matrix ensembles. First we consider
the real symmetric matrices. In full generality we show
that the linear level repulsion is a very robust phenomenon, and
is present always when the matrix element distribution functions
are regular at zero level, independent of other details. In particular,
we treat specific cases and work out exact analytic results in closed form
for the following ensembles: (i) Gaussian distribution (but generally
with different widths), (ii) box (uniform) distribution, (iii) Cauchy-Lorentz
distribution, (iv) exponential distribution. If the matrix element
distribution is singular at zero level, e.g. a power law times
exponential, we encounter the phenomenon of fractional power law level
repulsion which has been found in dynamical system by Prosen and Robnik
(1993,1994) and is related to sparsed matrices and KAM-type systems.
A similar analysis applies for the Hermitian complex matrices, where the
level repulsion is quadratic if the distribution of matrix elements is
regular at zero level. Moreover, we treat also non-normal real symmetric
matrices, where in general the analysis is much more difficult, because
the level repulsion (small
for a number of different random matrix ensembles. First we consider
the real symmetric matrices. In full generality we show
that the linear level repulsion is a very robust phenomenon, and
is present always when the matrix element distribution functions
are regular at zero level, independent of other details. In particular,
we treat specific cases and work out exact analytic results in closed form
for the following ensembles: (i) Gaussian distribution (but generally
with different widths), (ii) box (uniform) distribution, (iii) Cauchy-Lorentz
distribution, (iv) exponential distribution. If the matrix element
distribution is singular at zero level, e.g. a power law times
exponential, we encounter the phenomenon of fractional power law level
repulsion which has been found in dynamical system by Prosen and Robnik
(1993,1994) and is related to sparsed matrices and KAM-type systems.
A similar analysis applies for the Hermitian complex matrices, where the
level repulsion is quadratic if the distribution of matrix elements is
regular at zero level. Moreover, we treat also non-normal real symmetric
matrices, where in general the analysis is much more difficult, because
the level repulsion (small ![]() behaviour of
behaviour of ![]() ) depends not only
on the distribution of matrix elements at zero level, but on the
entire behaviour of the matrix element distribution function.
In the special case of Gaussian matrix element distribution functions
with different widths we again surprisingly find linear level repulsion,
but the details of small
) depends not only
on the distribution of matrix elements at zero level, but on the
entire behaviour of the matrix element distribution function.
In the special case of Gaussian matrix element distribution functions
with different widths we again surprisingly find linear level repulsion,
but the details of small ![]() behaviour of the level spacing distribution
are quite subtle and require more elaborate analysis.
Finally, we also comment on the case of the mixed type systems,
with partially regular and partially chaotic classical dynamics.
behaviour of the level spacing distribution
are quite subtle and require more elaborate analysis.
Finally, we also comment on the case of the mixed type systems,
with partially regular and partially chaotic classical dynamics.
References and Literature for Further Reading
[1] S. Grossmann and M. Robnik, J. Phys. A: Math. Gen 40 (2007) 409-421.
[2] S. Grossmann and M. Robnik, J. Phys. A: Math. Gen 40 (2007) submitted.
[3] G. Vidmar, H.-J. Stöckmann, M. Robnik, U. Kuhl, R. Höhmann and S. Grossmann, J. Phys. A: Math. Gen 40 (2007) submitted.
[4] H.-J. Stöckmann, Quantum Chaos - An Introduction (1999) (Cambridge University Press).
[5] M. Robnik, Nonlinear Phenomena in Complex Systems (Minsk) 1 (1998) No 1, 1-22.
[6] T. Guhr, A. Müller-Groeling and H.A. Weidenmüller, Phys. Rep. 299 Nos. 4-6(1998) 189-428.
[7] O. Bohigas, M.-J. Giannoni and C. Schmit, Phys. Rev. Lett. 52 (1984) 1.
[8] G. Casati, F. Valz-Gris and I. Guarneri, Lett. Nuovo Cimento 28 (1980) 279.
[9] M. L. Mehta, Random Matrices (1991) (Boston: Academic Press).
[10] T. Prosen and M. Robnik, J. Phys. A: Math. Gen 26 (1993) 2371.
[11] T. Prosen and M. Robnik, J. Phys. A: Math. Gen 27 (1994) 8059.
[12] T. Prosen and M. Robnik, J. Phys. A: Math. Gen 26 (1993) 1105.
[13] T. Prosen and M. Robnik, J. Phys. A: Math. Gen 32 (1999) 1863.
[14] H. Hasegawa, M. Robnik and G. Wunner, Prog. Theor. Phys. Supp. (Kyoto) 98 (1989) 198-286.
[15] M. Robnik, J. Phys. A: Math. Gen 14 (1981) 3195-3216.
[16] M. Robnik, J. Physique Colloque C2 43 (1982) 45.
[17] M. Robnik and V. G. Romanovski, Nonlinear Phenomena in Complex Systems (Minsk) 5 (2002) No4 445.
[18] M. Robnik and V. G. Romanovski, J. Phys. A: Math. Gen. 36 (2003) 7923.
[19] H. Ruder, G. Wunner, H. Herold and F. Geyer Atoms in Strong Magnetic Fields (1994) (Berlin: Springer).
Assume that all solutions in a neighborhood of an equilibrium point
of a two-dimensional autonomous system of ODE's are periodic.
We say that the system is isochronous in a neighborhood of the equilibrium point if
the period of oscillations is the same for all solutions near the point.
In the talk we present some methods to study isochronicity of oscillations in
2-dim autonomous systems which right hand sides are analytic functions.
References and Literature for Further Reading
[1]
J. Chavarriga and M. Sabatini,
Qual. Theory of Dyn. Systems 1 (1999) 1-70
[2] M. Robnik and V. G. Romanovski,
J. Phys. A: Math. Gen. 32 (1999) 1279-83
[3] C. Christopher, P. Mardešić and C. Rousseau,
J. Dynam. Control Systems 10 (2004) 501-525
[4] A. R. Chouikha, V. G. Romanovski and X. Chen, J. Phys. A:
Math. Theor. 40 (2007) 2313-2327
[5] V. G. Romanovski, X. Chen and Z. Hu, J. Phys. A:
Math. Theor. 40 (2007) 5905-5919
[6] M. Urabe,
Arch. Ration. Mech. Anal. 11 (1962) 27-33
The formalism of raising and lowering operators is developed for the difference operator analogue of a quantum harmonic oscillator which acts on functions on a discrete support. The grid under consideration is a mixed version of an equidistant lattice and a basic linear grid. Several properties of the grid are described. The grids under consideration are referred to by the name unitary linear lattices. The ladder difference operators are derived and compared with the continuum situation. The arising spectral problems for these operators are dealt by using the theory of bilateral Jacobi operators in weighted
![]() spaces.
spaces.
References and Literature for Further Reading
[1] R. N. Álvarez, D. Bonatsos and Yu. F. Smirnov, ![]() -Deformed vibron model for diatomic molecules, Physical Review A. 50 (1994) 1088-1095.
-Deformed vibron model for diatomic molecules, Physical Review A. 50 (1994) 1088-1095.
[2] R. Askey, S. K. Suslov, The ![]() -harmonic oscillator and the Al-Salam and Carlitz polynomials, Letters in Mathematical Physics 29 (1993) No. 2, 123-132.
-harmonic oscillator and the Al-Salam and Carlitz polynomials, Letters in Mathematical Physics 29 (1993) No. 2, 123-132.
[3] C. Berg, M.E.H. Ismail, Q-Hermite polynomials and classical orthogonal polynomials, Can. J. Math. 48 (1996) 43-63.
[4] C. Berg, A. Ruffing, Generalized ![]() -Hermite Polynomials, Communications in Mathematical Physics 223 (2001) 1, 29-46.
-Hermite Polynomials, Communications in Mathematical Physics 223 (2001) 1, 29-46.
[5] A. Ruffing, J. Lorenz, K. Ziegler, Difference Ladder Operators for a Harmonic Schrödinger Oscillator Using Unitary Linear Lattices, Journal of Computational and Applied Mathematics 153 (2003), 395-410.
References and Literature for Further Reading
[1] Ashcroft FM, Rorsman P. (1989) Electrophysiology of the pancreatic beta-cell. Prog Biophys Mol Biol. 54(2):87-143.
[2] Speier S, Rupnik M. (2003) A novel approach to in situ characterization of pancreatic beta-cells. Pflugers Arch. 446(5):553-8.
[3] Meneghel-Rozzo T, Rozzo A, Poppi L, Rupnik M. (2004) In vivo and in vitro development of mouse pancreatic beta-cells in organotypic slices. Cell Tissue Res. 316(3):295-303.
[4] Speier S, Gjinovci A, Charollais A, Meda P, Rupnik M. (2007) Cx36-mediated coupling reduces beta-cell heterogeneity, confines the stimulating glucose concentration range, and affects insulin release kinetics. Diabetes. 56(4):1078-86.
As is well known, different types of localization phenomena, such as
dynamical localization, localization on invariant tori, localization on
unstable periodic orbits, appear simultaneously in the quantum system
whose classical phase space is composed of regular and chaotic
components. Each has its own origin and a different classical
invariant set as its support. However, they coexist in a single phase
space, one would expect that they are affected by each other and
correlated under a certain consistent rule. In the present talk, we
will show that a strong interplay indeed exists between dynamical
localization and localization on invariant tori, and discuss how
one quantum effect is suppressed by another quantum effect.
References and Literature for Further Reading
[1] E. Ott, T. M. Antonsen, Jr., J. D. Hanson, Phys. Rev. Lett. 23, (1984) 2187-2190; S. Adachi, M. Toda, K. Ikeda, Phys. Rev. Lett. 61, (1984) 659-661.
[2] F. Grossmann, T. Dittrich, P. Jung, P. Hänggi, J. Stat. Phys. 70, (1993) 229-245.
[3] A. Bäcker, R. Ketzmerick, A.G. Monastra, Phys. Rev. Lett. 94 (2005) 054102 (4pages).
[4] A. Ishikawa, A. Tanaka, A. Shudo, Quantum Suppression of Chaotic Tunneling, J. Phys. A, 40 (2007) F1-F9.
Transitions in the cardio-respiratory synchronization ratio in healthy
subjects at rest will be presented. The state of exchange of energy and
matter of the cardiovascular system will be considered and data from
anaesthesia (with low exchange rate), rest (moderate exchange) and
exercise (high exchange) will be discussed. The investigation has been
extended to studies of synchronization at high altitude, simulated by
the breathing of different oxygen concentrations. The implications for
the pressurisation of aircraft will be considered.
Scattering theory, originally developed in nuclear physics [1], meanwhile has found numerous applications also in mesoscopic systems [2]. One example is the study of transport properties through open quantum dots. For such systems it is a highly non-trivial task, however, to determine the confining potential, the number of modes in the attached channels, etc., from the geometry of the gate electrodes.
Here microwave resonators are an alternative. For flat resonators there is a complete equivalence to the corresponding quantum dot system, as long as electron-electron interactions are negligible [3]. In contrast to real quantum dot systems measurements are performed at room temperatures and not in the mK regime, and system sizes are of some centimetres and not of sub-microns, with the consequence that the geometry is perfectly controllable.
This allows checks of predictions of scattering theory which
are not accessible otherwise. A number of examples will be given. In
addition a look into the systems is possible thus allowing the study
of the flow through the system, of statistics and
distributions of vortices etc.
References and Literature for Further Reading
[1] T. Guhr, A. Müller-Gröling, H. Weidenmüller, Phys. Rep. 299, 189 (1998).
[2] C. Beenakker, Rev. Mod. Phys. 69, 731 (1997).
[3] H.-J. Stöckmann, Quantum Chaos - An Introduction, Cambridge UP 1999.
The Husimi distribution, which is defined
on the phase space, is a useful tool to investigate
dynamical properties of quantum systems in comparison
with classical dynamics. After a short review of the
standard Husimi distribution, I will discuss its
generalization to many-body problems. Delocalization
of the generalized Husimi distribution is related
not only to chaoticity of the underlying classical
dynamics, but also to the degree of entanglement
of the state. I will also show an algebraic method
to calculate the moments of the generalized Husimi
distributions with use of the group representation
theory.
With this method, one can systematically
generate a lot of entanglement measures
including well-known ones such as the concurrence and the 3-tangle.
References and Literature for Further Reading
[1] K. Husimi, Proc. Phys. Math. Soc. Japan 22 (1940) 264-314.
[2] A. Sugita, J. Phys. A: Math. Gen 36 (2003) 9081-9103.
[3] A. Sugita, J. Phys. A: Math. Gen 35 (2002) L621-L626.
[4] A. Sugita and H. Aiba, Phys. Rev. E 65 (2002) 036205.
I discuss characteristic dynamics of a system, which consists of classical and quantum subsystems strongly coupling with each other. Typically, the quantum subsystem is composed with light and fast particles, while heavy and slow particles constitute the classical subsystem. Such systems are quite ubiquitous, since molecules are more or less approximated in terms of this mixed quantum-classical representation, with nuclei being heavy and classical particles and electrons being light and quantum particles. More explicitly, the separation of electronic and nuclear motions based on this idea constitutes the heart of the so-called Born-Oppenheimer approximation, which is now the standard concept in material sciences.
In the Born-Oppenheimer view, nuclei are supposed to propagate in time (either classically or quantum mechanically) on a potential energy function, which is given as electronic energy at parametrically fixed nuclear coordinates. In particular, classical trajectory studies of nuclear motion on the Born-Oppenheimer potential
energy surfaces (electronic energy) are now one of the standard methods of molecular dynamics. In
particular, such a description becomes inevitable
for large molecular systems such as those in protein dynamics. However, as soon as more than a single potential
energy surface is involved in the dynamics due to "nonadiabatic" coupling, such
a naive application of classical mechanics lacks a theoretical foundation.
This is a classic, fundamentally important, yet highly practical issue in the
foundation of molecular science. To cope with this, I propose a generalization of
classical mechanics that provides a "classical" path even in cases where
multiple potential energy surfaces are involved in a single event and the
Born-Oppenheimer approximation breaks down. This generalization is made by
diagonalization of the matrix representation of nuclear forces in nonadiabatic
dynamics and is derived in terms of mixed quantum-classical representation of
the electron-nucleus entangled Hamiltonian [1]. Quantum fluctuation and possible chaos manifested in the classical subsystem will be discussed.
References and Literature for Further Reading
[1] K. Takatsuka, J. Chem. Phys. 124
(2006) 064111.
and many references cited therein.
Dispersion interactions (also known as the van der Waals or Casimir interactions) are ubiquitous and are a relevant phenomenon in a variety of fields such as biological systems, nanotechnology and thin films. As these interactions are generally non additive and depend on the geometry of the system in a complex way, their calculation for arbitrary or even simple geometries is not straightforward. I will present various aspects of their calculation. First I will present a numerical method suitable for arbitrary geometries of constant dielectric response. I will then discuss the equivalence of approaching the calculation either from the view of matter fluctuations or from the viewpoint of field fluctuations on a specific example of plane parallel geometries. I will conclude by presenting a model self-consistent calculation of density profiles in a thin film where the matter interacts solely via dispersion forces.
References and Literature for Further Reading
[1] Mahanty J and Ninham BW 1976 Dispersion forces (Academic Press, New York).
[2] Veble G and Podgornik R 2007 Phys. Rev. B 75 155102.
[3] Veble G and Podgornik R 2007 Eur. Phys. J. E (in print).
A new RMT study of ![]() energy level statistics is presented. It is expected
to describe the quantum Hamilton systems whose
classical dynamics is of mixed type. In the semiclassical limit the Berry-Robnik (BR) statistics applies, while at larger
values of the effective Planck constant
energy level statistics is presented. It is expected
to describe the quantum Hamilton systems whose
classical dynamics is of mixed type. In the semiclassical limit the Berry-Robnik (BR) statistics applies, while at larger
values of the effective Planck constant
![]() one sees
deviations from BR at nearby levels due to localisation and tunnelling effects.
First the general perturbation leading to all-to-all level couplings
is considered and second, the influence of
the tunneling between regular and chaotic states on spectra is modelled.
one sees
deviations from BR at nearby levels due to localisation and tunnelling effects.
First the general perturbation leading to all-to-all level couplings
is considered and second, the influence of
the tunneling between regular and chaotic states on spectra is modelled.
An analytic expression in a closed form for a two-level RMT model is derived
and compared with a ![]() -level one, which has been done numerically. The coupling
between the levels (the off-diagonal matrix elements) is assumed
to be Gaussian distributed. In antenna (general) distorted systems our
two-level model describes
the features of large matrices very well.
Small
-level one, which has been done numerically. The coupling
between the levels (the off-diagonal matrix elements) is assumed
to be Gaussian distributed. In antenna (general) distorted systems our
two-level model describes
the features of large matrices very well.
Small ![]() result for fully chaotic system is in agreement with experiment.
In the treatment of the tunnelling only the regular
and chaotic states are coupled. The two-level model is still good enough and
is predicted (with an improvement) to apply in mixed type systems at low energies. The
proposed level spacing distribution function has two parameters, the
BR parameter
result for fully chaotic system is in agreement with experiment.
In the treatment of the tunnelling only the regular
and chaotic states are coupled. The two-level model is still good enough and
is predicted (with an improvement) to apply in mixed type systems at low energies. The
proposed level spacing distribution function has two parameters, the
BR parameter ![]() , characterising the classical phase space, and
the coupling (antenna distortion or tunnelling) parameter
, characterising the classical phase space, and
the coupling (antenna distortion or tunnelling) parameter ![]() ,
describing the coupling between the states.
,
describing the coupling between the states.
References and Literature for Further Reading
[1]Vidmar G, Stöckmann H.-J., Robnik M, Kuhl U, Höhmann R and Grossmann S 2007
submitted to J. Phys. A: Math. Theor.
[2] Stöckmann H.-J. 1999 Quantum Chaos - An Introduction
(Cambridge University Press).
[3]Haake F 2001 Quantum Signatures of Chaos (Berlin: Springer)
[4]Berry M V and Robnik M 1984 J. Phys. A: Math. Gen.17 2413-2421
[5]Prosen T and Robnik M 1994 J. Phys. A: Math. Gen. 27 8059-8077
[6]Haake F, Kuś M, Šeba P, Stöckmann H-J and
Stoffregen U 1996, J. Phys. A: Math. Gen. 29 5745-5757
[7]Podolskiy V A and Narimanov E E 2003 Phys. Rev. Lett. 91 263601-1
[8]Grossmann S and Robnik M 2007
J. Phys. A: Math. Theor. 40 409-421
[9]Grossmann S and Robnik M 2007
submitted to J. Phys. A: Math. Theor.
For all we know the laminar states in planar shear flows and in pipe flow are linearly stable for arbitrarily large shear rates. On the other hand, finite perturbations can trigger a transition to turbulent flow. As early as 1989 it was suggested [1] that this turbulent motion might be transient rather than constituting a persistent feature of the flow. Very recently high-resolution numerical and experimental studies [2] confirmed this picture. This finding raises intriguing questions regarding the nature of the edge of chaos which separates the phase-space region with turbulent dynamics from the region where trajectories smoothly decay to the stable laminar state. An analysis of this boundary in a 9-mode Galerkin model revealed that even the dynamics restricted to this boundary exhibits transient chaos [3].
I will briefly review these recent developments, and present a 2d
model providing insight into the morphology of the phase boundary and
its dynamics.
References and Literature for Further Reading
[1] U. Brosa, J. Stat. Phys. 55 (1989) 1303-1312.
[2] R.R. Kerswell, Nonlinearity 18 (2005) R17-R44;
B. Eckhardt, T.M. Schneider, B. Hof, and J. Westerweel,
Ann. Rev. Fluid Mech. 39 (2007) 447-468.
[3] J.D. Skufca, J.A. Yorke, and B. Eckhardt,
Phys. Rev. Lett. 96 (2006) 174101.
The aggregation of particles has attracted considerable interest as a
problem of non-equilibrium physics. It is observed not only in many
physical and chemical systems[1] but also in biological
and social systems[2]. In the case of particle aggregation
in a multiphase system, particle motion can interact with phase boundary
motion. For example, surfactant molecules in an oil-water system affect the
motion of the oil-water phase boundary[3]. In this case, by changing the
concentration of the surfactant, various structures are formed in the
microemulsion system such as spheres, cylinders, and lamellae[4].
In order to understand the dynamical properties induced by the interaction between the particle and phase boundary motions, a definite and simple picture of the collective motion of particles should be developed. We consider the motion of the air front (i.e., air-water boundary) during water evaporation as an example of phase boundary motion. When granular particles exist in the water phase, they can prevent the motion of the air front. It should be noted that the role of the particles in the air front motion differs significantly depending on the particle concentration in the system. When the concentration is quite low, the particles are treated individually as an impurity that induces the pinning effect on the air front motion. On the other hand, at a high concentration, the system is packed with the particles. Accordingly, the granular particles are treated as a porous medium, and the dynamics of the air front motion is considered as the dynamics of invasion percolation[5]. Evidently, there is a huge gap in the treatment of granular particles between low and high particle concentration cases. Therefore, at the intermediate concentration, it is difficult to characterize the collective motion of particles.
Recently, we have studied the formation of the labyrinthine pattern which
corresponds to
a spatial distribution of aggregated granular particles at the intermediate
concentration. The pattern is produced by the air front
that sweeps granular particles during the evaporation process of the
water-granule system.
In this talk, we show experimental results[6] and three types of modeling
for the pattern formation:
(a) reaction-diffusion type equations[7,8],
(b) molecular dynamics for the motion of the particles[9],
and (c) cell automaton[10].
References and Literature for Further Reading
[1] T. Vicsek, Fractal Growth Phenomena, World Scientific,
Singapore (1992)
[2] F. Schweitzer, Brownian Agents and Active Particles,
Springer Verlag, Berlin (2003)
[3] T. Kawakatsu and K. Kawasaki, Physica A 167 (1990) 690-735
[4] S. A. Safran, Statistical Thermodynamics of Surfaces, Interfaces,
and Membranes,
Addison-Wesley Pub., Massachusetts (1994)
[5] D. Stauffer and A. Aharony, Introduction to Percolation Theory ,
Taylor & Francis, London (1994)
[6] Y. Yamazaki and T. Mizuguchi, J. Phys. Soc. Jpn.
69 (2000) 2387-2390.
[7] T. Iwashita, Y. Hayase and H. Nakanishi, J. Phys. Soc. Jpn.
74 (2005) 1657-1660.
[8] M. Mimura T. Watanabe and Y. Yamazaki, unpublished.
[9] S. Komura and Y. Yamazaki, to be submitted in J. Phys. Soc.
Jpn.
[10] Y. Yamazaki, S. Komura and K. Suganuma, J. Phys. Soc. Jpn.
75 (2006) 043001 (4pages).
References and Literature for Further Reading
[1] J. Emerson, Y.S. Weinstein, M. Saraceno, S. Lloyd, D.G. Cory, Pseudo-unitary random operators for quantum information processing, Science
302 2098 (2003).
[2] R. Oliveira, O.C.O. Dahlstein, M.B. Plenio, Generic entanglement can be generated efficiently, Phys. Rev. Lett. 98, 130502 (2007).
[3] M. Žnidarič, Entanglement of random vectors, J. Phys. A 40, F105 (2007).
[4] M. Žnidarič, Optimal two qubit gate for generation of random bipartite entanglement, preprint quant-ph/0702240.