


Next: SHORT REPORTS
Up: programme
Previous: INVITED LECTURERS AND SPEAKERS
The following are extended abstracts of all invited lectures,
each one 60 minutes long. The ordering is alphabetical according to
the surname of the lecturer, whilst his or her lectures are
ordered temporaly in accordance with appearance in the programme.
We expect only a few minor updates which will be done in due course.
On Friday, 2 July 1999, the whole daily programme will be devoted
to the Japan-Slovenia Seminar on Chaos Science, which
is fully and separately displayed on the next page. The Organizing
Committee thanks the Japan Society for the Promotion of Science
for the full financial support of this Seminar, which is a part
of the scientific programme of the School/Conference.
JAPAN-SLOVENIA SEMINAR ON CHAOS SCIENCE
(A Special Session at Maribor, Slovenia, 2 July 1999)
Main Talks (50 minutes for each)
- 1. Yoji Aizawa
- Ergodic Properties of Non-stationary
Chaos
- 2. Tomaz Prosen
- Quantum Poincaré Mapping
- 3. Yoshiki Kuramoto
- Turbulence with Multiscaling in Large
Assemblies of Oscillators
- 4. Marko Robnik
- Topics in Quantum Chaos of Generic Systems
Intermission for Lunch
- 5. Hiroshi Hasegawa
- Information Theoretical Basis of Random
Matrix Distributions
- 6. Janko Gravner
- Growth Phenomena in Cellular Automata
- 7. Mitsugu Matsushita
- Formation of Colony Patterns by a
Bacterial Cell Population
- 8. Aneta Stefanovska
- Topics in Nonlinear Dynamics in
the Human Cardiovascular
System
The Organizing
Committee thanks the Japan Society for the Promotion of Science
for the full financial support of this Seminar, which is a special programme
embedded into the scientific programme of the School/Conference.
Long time tails in N-body Hamiltonian systems
Yoji Aizawa
Department of Applied Physics, Faculty of Science and
Engineering,
Waseda University, Tokyo, Japan
One of the most striking phenomena in chaotic dynamics is the
appearance of the long time tails such as the 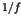 fluctuations [1,2]. In the nearly integrable Hamiltonian systems, the
long time tails are universally generated due to the stagnant
motions near the invariant KAM tori;
fluctuations [1,2]. In the nearly integrable Hamiltonian systems, the
long time tails are universally generated due to the stagnant
motions near the invariant KAM tori;
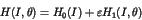 |
(1) |
Here the parameter 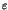 stands for the perturbation to
the integrable Hamiltonian
stands for the perturbation to
the integrable Hamiltonian 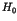 . An important theorem
(Nekhoroshev,1977) explained that the residence time
. An important theorem
(Nekhoroshev,1977) explained that the residence time 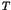 in the
stagnant layer obeys [3],
in the
stagnant layer obeys [3],
![\begin{displaymath}
T\simeq \frac{1}{\varepsilon} \exp[\varepsilon ^{-b}]
, (\varepsilon \ll 1)
\end{displaymath}](img7.png) |
(2) |
where 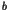 is a positive constant determined by the unperturbed
Hamiltonian
is a positive constant determined by the unperturbed
Hamiltonian 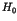 in Eq.(1).
in Eq.(1).
The significant point in Eq.(2) is that the divergence of 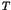 does not obey the inverse power law but exhibits an essential
singularity when
does not obey the inverse power law but exhibits an essential
singularity when 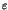 goes to zero. In 1980's, the
origin of such singularity was studied in terms of the scaling
theory for the stagnant layers mentioned above, where the
hierarchical structure of resonant tori (islands around island)
plays an essential role to induce the long time tails in
dynamical quantities. The stagnant layer theory (Aizawa , 1989)
demonstrated that the distribution of the residence time, say
P(T), obeys a universal law [2],
goes to zero. In 1980's, the
origin of such singularity was studied in terms of the scaling
theory for the stagnant layers mentioned above, where the
hierarchical structure of resonant tori (islands around island)
plays an essential role to induce the long time tails in
dynamical quantities. The stagnant layer theory (Aizawa , 1989)
demonstrated that the distribution of the residence time, say
P(T), obeys a universal law [2],
![\begin{displaymath}
P(T) \simeq \frac{1}{T[\log T]^c} , (T \gg 1)
\end{displaymath}](img9.png) |
(3) |
where 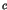 is a positive constant larger than unity. Equation(3)
has been confirmed by simulations (Aizawa et al, 1989). The
essential singularity in Eq.(2) reflects the onset of
is a positive constant larger than unity. Equation(3)
has been confirmed by simulations (Aizawa et al, 1989). The
essential singularity in Eq.(2) reflects the onset of 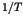 divergence in Eq.(3). The point is that the distribution is not
normalizable,i.e., a typical infinite measure.
divergence in Eq.(3). The point is that the distribution is not
normalizable,i.e., a typical infinite measure.
Firstly, my lecture will be directed to the review of the
stagnant layer theory and some numerical evidence in many body
systems. Secondly, the onset of a new type of long time tails
will be discussed carrying out with the clustering motions in
N-body systems with short range attractive forces, where the
distribution of the trapping time 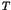 obeys another universal law,
obeys another universal law,
![\begin{displaymath}
P(T) \simeq T^{- \beta -1}\exp[-aT^{- \beta}]
\end{displaymath}](img12.png) |
(4) |
where 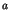 is a positive constant which depends on the size of
cluster. The regularly varying part of Eq.(4) denotes the tail with
is a positive constant which depends on the size of
cluster. The regularly varying part of Eq.(4) denotes the tail with
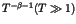 , and the parameter
, and the parameter 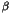 depends
on the dimension of the cluster under consideration. The stability of the
clustering motions will be explained based on the long time tail
of Eq.(4).
depends
on the dimension of the cluster under consideration. The stability of the
clustering motions will be explained based on the long time tail
of Eq.(4).
References
![$[1]$](img16.png) Aizawa Y 1989a Prog.Theor.Phys.Suppl. 99149; Aizawa Y
1999 Chaos, Soliton and Fractals (in press); Tanaka K and
Aizawa Y 1993 Prog.Theor.Phys. 90(3)
Aizawa Y 1989a Prog.Theor.Phys.Suppl. 99149; Aizawa Y
1999 Chaos, Soliton and Fractals (in press); Tanaka K and
Aizawa Y 1993 Prog.Theor.Phys. 90(3)
![$[2]$](img17.png) Aizawa Y 1989b Prog.Theor.Phys. 81(2) 249; Aizawa Y
et al 1989c Prog.Theor.Phys.Suppl. 98
37; Aizawa Y 1995 J.Korean Phys.Soc. 28 310; Aizawa Y
1991 Dynamical Theory of
Aizawa Y 1989b Prog.Theor.Phys. 81(2) 249; Aizawa Y
et al 1989c Prog.Theor.Phys.Suppl. 98
37; Aizawa Y 1995 J.Korean Phys.Soc. 28 310; Aizawa Y
1991 Dynamical Theory of  spectral
chaos, eds. Musha.T et al,pp483-487
spectral
chaos, eds. Musha.T et al,pp483-487
![$[3]$](img19.png) Nekhoroshev N N 1977 Russ.Math.Surveys 32 1
Nekhoroshev N N 1977 Russ.Math.Surveys 32 1
Ergodic properties of non-stationary chaos
Yoji Aizawa
Department of Applied Physics, Faculty of Science and
Engineering,
Waseda University,
Tokyo, Japan
Non-stationary chaos is a universal phenomenon in non-hyperbolic
dynamical systems.
Basic problems regarding the non-stationarity are discussed from
ergodic-theoretical viewpoints.
By use of a simple system, it is shown that ``the law of large
number'' as well as ``the law of small number'' break down in the
non-stationary regime.
The non-stationarity in dynamical systems proposes a crucial problem
underlying in the transitional region between chance and
necessity(onceness and recurrence), where non-observable processes
behind reality interplay with observable ones.
The incompleteness of statistical ensembles is discussed from the
Karamata's theory.
Finally, the significance of the stationary/non-stationary interface
is emphasized in relation to the universality of 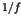 fluctuations.
fluctuations.
References
Aizawa Y 1989 Prog.Theor.Phys. 81 pp249-253
Aizawa Y et al 1989 Prog.Theor.Phys. Suppl. 98
Aizawa Y 1995 J.Korean Phys.Soc. 28 pp310-314
Aizawa Y 1991 ICNF,eds Musha T et al pp483-487
Kurosaki S and Aizawa Y 1997Prog.Theor.Phys. 98
pp783-793
Yuri M 1995 Indag.Math.N.S. 6 pp355-383
Yuri M 1996 Nonlinearity 9 pp1439-1461
Yuri M 1997 Erg.Th.and Dynam.Sys. 17 pp977-1000
Aizawa Y 1989 Studies of Dynamical Systems,eds Aoki N(World
sci.) pp182-191
Kikuchi Y and Aizawa Y 1990 Prog.Theor.Phys. 84
pp563-567
Kikuchi Y and Aizawa Y 1990 Prog.Theor.Phys 84
pp1014-1018
Aizawa Y 1984 Prog.Theor.Phys. 72 pp659-661
Aizawa Y and Kohyama T 1984 Prog.Theor.Phys. 71
pp847-850
Aizawa Y 1989 Prog.Theor.Phys.Suppl. 99 pp149-164
Aizawa Y 1993 Prog.Theor.Phys. 90 pp547-567
Aizawa Y 1998 International Journal of Computing Anticipatory
Systems 2 pp235-249
Universal aspects in level statistics of oval billiards
Yoji Aizawa, Hironori Makino and Mayuko Morita
Department of Applied Physics, Faculty of Science and
Engineering,
Waseda University, Tokyo, Japan
We studied the energy level statistics for one parameter
family of oval billiards whose classical phase space consists
of some regular and some irregular components. As the parameter
is varied, a transition from an integrable system to a
strongly chaotic one occurs with successive bifurcations. We
applied the Berry-Robnik formulae to the level-spacing
distributions for a variety of shapes of quantum oval
billiards and found some striking effects of bifurcations in
the classical mechanical systems on the level-spacing
distributions. The validity of the Berry-Robnik formula is
also checked for those shapes of the oval billiard for which
there exist two separated chaotic components in the phase
space [1]. However, the Berry-Robnik formula is not
available for the
entire energy range, especially in the lower energy region the Brody-like
behaviors have been often observed until now [2,3]. In the latter
part of our talk, we will discuss that the transition from the Brody
distribution
to the Berry-Robnik formula universally occurs for all parameter regime
of our model, and the detailed process of the transition near the bifurcation
point will be reported.
References
[1]Makino H, Harayama T and Aizawa Y 1999 Phys.Rev.E 59 4026
[2]Robnik M and Prosen T 1997 J. Phys. A:Math.Gen. 30
8787
[3]Prosen T 1998 J. Phys. A:Math.Gen. 31 7023
Complex dynamics of a ``simple'' mechanical system:
the parametrically excited pendulum
Steven R. Bishop
Center for Nonlinear Dynamics and its Applications,
University College London, UK
A planar pendulum is perhaps the simplest and most quoted example of a
dynamical system, yet when driven its simplicity of description belies a
range of complex dynamical motions. If driven vertically at the pivot, a
pendulum which can freely move in the plane exhibits equilibrium states,
periodic solutions, as well as chaotic motions, all of which can easily be
seen in a mechanical experiment. Miles (1989) produced an excellent overview
of the basic, qualitative dynamics but research interest is not yet
exhausted with some recent results investigating the topological structure
of phase space (Clifford and Bishop 1994) and the stability of the inverted
state (Clifford and Bishop 1996).
The dynamics of the pendulum can be envisaged a particle moving in a
cosinusoidal potential energy function. Small oscillations correspond to
periodic motions within the well while rotations lead to escape from the
local potential well between 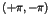 . For small driving amplitudes the
downward hanging state forms a stable equilibrium of the model system which
becomes unstable in a series of zones. Numerically we can follow the stable
solutions and follow bifurcations to plot the zones in parameter space in
which the various solutions exist where typically the boundary between
solutions is fractal and as a consequence the resulting dynamics is complicated
even for this 'simple' system.
In addition, combining a mixture of methods to locate unstable orbits, and
developing robust methods for control even in the presence of noise, means
that now we are able to select a desired solution from a large selection of
unstable motions onto which the system can be controlled (Bishop et.al.
1996) without globally changing the system parameters.
. For small driving amplitudes the
downward hanging state forms a stable equilibrium of the model system which
becomes unstable in a series of zones. Numerically we can follow the stable
solutions and follow bifurcations to plot the zones in parameter space in
which the various solutions exist where typically the boundary between
solutions is fractal and as a consequence the resulting dynamics is complicated
even for this 'simple' system.
In addition, combining a mixture of methods to locate unstable orbits, and
developing robust methods for control even in the presence of noise, means
that now we are able to select a desired solution from a large selection of
unstable motions onto which the system can be controlled (Bishop et.al.
1996) without globally changing the system parameters.
References
Bishop, S.R., Xu, D. and Clifford, M.J. 1996 Flexible control of
the parametric pendulum, Proc. Roy. Soc. Lond. A452, 1-18.
Capecchi, D. and Bishop, S.R. 1994 Periodic oscillations and
attracting basins for a parametrically excited pendulum, Dynamics and
Stability of Systems 9, No.2, 123-143.
Clifford, M.J. and Bishop, S.R. 1994 Bifurcational precedences for
parametric escape from a symmetric potential well, International J.
Bifurcation & Chaos 4, No.3, 623-630.
Clifford, M.J. and Bishop, S.R. 1996 Locating oscillatory orbits of
the parametrically excited pendulum, J. Austral. Math. Soc. Series B 37,
309-319.
Clifford, M.J. and Bishop, S.R. 1998 Inverted oscillations of a
driven pendulum, Proc. Roy. Soc. Lond. A 454, 2811-2817.
Miles, J. (1989) The pendulum from Huygens' Horologium to symmetry
breaking and chaos, in Theoretical and Applied Mechanics, edited by P.
Germain, M. Piau and D. Caillerie, Elsevier Science: North Holland, pp
193-215.
The nonlinear dynamics of ship roll and capsize
Steven R. Bishop
Center for Nonlinear Dynamics and its Applications,
University College London, UK
Ensuring that a ship can resist capsize when confronted with steep waves is
an important consideration during design. Unfortunately, current ship
design practices, due their reliance on ad hoc, empirical and static-type
criteria of stability, are grossly inadequate to address the dynamic
effects incurred on the ship due to wave action where the capsize process
is both nonlinear and transient. The need for suitable dynamic capsize
criteria is accentuated by the proximity of typical ocean wave frequencies
to the natural roll frequency of many ships, which makes the possibility of
beam-sea resonance a key feature of any worst-case scenario.
Due to the nonlinearity of the accompanying restoring force multiple
steady-state roll responses can emerge, which can undergo further
complicated qualitative changes of their character sometimes even becoming
chaotic. More complex still can be the transient motions near to capsize
limits. Recent applications of the global geometrical techniques of
nonlinear dynamics and the associated problem of escape of a driven
oscillator from a potential well, have provided new possibilities for
advancing the state-of-the-art by achieving deeper understanding of the
phenomena that precede capsize. An interesting characteristic of these
phenomena is their remarkable robustness against gross changes in the forms
of stiffness and damping functions, which can yield simple and useful
design criteria against transient capsize.
We review here novel studies on ship capsize in beam seas, which have taken
place at the Centre for Nonlinear Dynamics and its Applications of
University College London. Large-amplitude ship rolling has been
investigated both theoretically and experimentally, under steady-state as
well as under transient conditions.
References
Thompson, J.M.T. 1989. Chaotic phenomena triggering the escape from a potential
well, Proc. R. Soc. Lond. A421,195-225.
Thompson, J.M.T. 1997. Designing against capsize in beam seas: Recent advances and new insights, Applied Mechanics Reviews 50,307-325.
Bifurcations, symmetry-breaking and pattern formation in
nonlinear systems
Tassos Bountis
Department of Mathematics and
Center for Research and Applications of Nonlinear Systems,
University of Patras, Greece
Lecture 1 : Bifurcations and Symmetry-Breaking in Nature
In these 3 lectures we shall review the basic concepts of stability analysis
and bifurcation theory for nonlinear systems, with emphasis on the
applications of these concepts to physics, chemistry and biology. We shall
begin with a discussion of the meaning of bifurcation and its
connection with symmetry-breaking in finite dimensional and
spatially extended (infinite dimensional) nonlinear systems.
As an example of the former, we examine chemical oscillations in closed,
continuously stirred reactors, while for the latter, we use the
Rayleigh-Benard experiment and reaction-diffusion systems from chemistry and
biology.
Concentrating then on the topic of bifurcations in finite dimensional systems
we will list the normal forms of the most commonly encountered types
of bifurcations : saddle-node, transcritical, pitchfork and Hopf.
Introducing the notions of codimension and transversality we will
consider which of these types are structurally stable, when additional
parameters and lower order terms are included in the dynamics.
The importance of nonlinear stability analysis will be emphasized in connection
with the study of center manifolds at bifurcation points.
Lecture 2 : Linear Stability of Spatially Extended Systems
In this lecture we review the main features of linear stability analysis
of steady states of spatially distributed systems, occurring in problems of
hydrodynamics and reaction-diffusion models of chemical and biological
systems. More specifically, we consider the Rayleigh-Benard problem
of a thin fluid layer heated from below and describe how one
can estimate the critical Rayleigh parameter 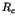 , at which the symmetry
of the spatially uniform state is broken by the formation of cylindrical
rolls.
Next, we discuss the onset of diffusion-driven or Turing instability
in reaction-diffusion systems and compare it with the onset of other types of
instability (caused e.g. by a Hopf bifurcation) on the example of the
Brusselator model. Symmetry-breaking and pattern formation will be
examined on diffusive, 2-variable models of competing species.
The dependence of the critical parameter value
, at which the symmetry
of the spatially uniform state is broken by the formation of cylindrical
rolls.
Next, we discuss the onset of diffusion-driven or Turing instability
in reaction-diffusion systems and compare it with the onset of other types of
instability (caused e.g. by a Hopf bifurcation) on the example of the
Brusselator model. Symmetry-breaking and pattern formation will be
examined on diffusive, 2-variable models of competing species.
The dependence of the critical parameter value  on a
characteristic length scale in such systems will be compared to the
absence of such a dependence in hydrodynamics.
on a
characteristic length scale in such systems will be compared to the
absence of such a dependence in hydrodynamics.
Lecture 3 : Wave Propagation in Excitable Media
In the last lecture, we turn our attention to the study of
reaction-diffusion equations describing excitable media. These are
systems composed of active units, like cells, possessing a certain
threshold of excitability, beyond which they can "fire" and transmit
their action potential to neighboring cells. They are described by
Fitzhugh-Nagumo (FHN) 2-variable partial differential equations in one or
more space dimensions.
Depending on the parameters of the FHN equations, action potentials can
travel in the form of localized waves, delivering their "message" along
the medium. At other parameters (and places) however, on the medium,
stationary pulses can either collapse or grow, forming a possible
"obstacle", hindering the propagation of action potential waves. We derive
analytical expressions for these stationary pulses and examine ways by
which their effect on the travelling waves can be controlled. The
connection of these phenomena with the occurrence of cardiac arrhythmia
is discussed, when the excitable medium under consideration is the
myocardium.
References
J. Guckenheimer and P. Holmes : Nonlinear Oscillations, Dynamical
Systems and Bifurcations of Vector Fields, Springer, Berlin, 1983.
S. Wiggins : Introduction to Applied Nonlinear Dynamical Systems
and Chaos, Springer, Berlin, 1990.
J. Murray : Mathematical Biology, Springer, Berlin, 1989.
A. S. Mikhailov : Foundations of Synergetics I : Distributed Active
Sytems, Springer, Berlin, 1990.
G. Nicolis and I. Prigogine : Exploring Complexity, W. H. Freeman,
New York, 1989.
G. Nicolis : Introduction to Nonlinear Science, Cambridge University
Press, 1997.
T. Bountis : Fundamental Concepts of Classical Chaos : Part I, Open
Syst. Inf. Dyn 3(1), 23 - 95, 1995.
T. Bountis, C. F. Starmer and A. Bezerianos : Wave Front Formation
and Stationary Pulses in Excitable Media, preprint, 1999.
Quantum localization and cantori in the stadium billiard
Giulio Casati
International Center for the study of Dynamical Systems,
Universitá degli Studi della Insubria, Como, Italy
We discuss the quantum behaviour of chaotic billiards which exhibit
classically diffusive behaviour. More precisely we consider the stadium
billiard and discuss how the interplay between quantum localization and
the rich structure of the classical phase space influences the quantum
dynamics. In particular we show how the presence of cantori in the
classical phase space affects the structure of the eigenfunctions and
the statistical properties of the eigenvalues. The analysis of this model
leads to new insight in the understanding of quantum properties of
classically chaotic systems.
References
Casati G and Prosen T 1999 Phys. Rev. E
59 R2516 and references therein.
Quantum Poincaré recurrences
Giulio Casati
International Center for the study of Dynamical Systems,
Universitá degli Studi della Insubria, Como, Italy
We study quantum chaos in open dynamical systems and show that it is
characterized by quantum fractal eigenstates located on the underlying
classical strange repeller. The states with longest life times typically
reveal a scar structure on the classical fractal set.We also show that
quantum effects modify the decay rate of Poincaré recurrences 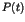 in
classical chaotic systems with mixed hierarchical structure of phase
space. It is shown that
in
classical chaotic systems with mixed hierarchical structure of phase
space. It is shown that 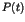 has an algebraic decay with a universal power
law
has an algebraic decay with a universal power
law 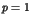 , due to tunnelling and localization effects. Experimental evidence
of such decay should be observable in mesoscopic systems and cold atoms.
, due to tunnelling and localization effects. Experimental evidence
of such decay should be observable in mesoscopic systems and cold atoms.
References
Casati G, Maspero G and Shepelyansky D L 1999 Phys. Rev. Lett.
82 524 and references therein.
Nonlinear dynamics and chaos in space plasmas
Abraham C.-L. Chian
Center for Subatomic Structure of Matter, University of Adelaide,
Australia
and National Institute for Space Research, São José dos Campos,
Brazil
We discuss the theory and observation of nonlinear phonomena in solar-system
plasmas. Plasma dynamics is governed by a variety of complex wave motions
resulting from the collective electrodynamic interactions involving plasma
field and plasma particles. Nonlinear wave-wave coupling in plasmas can occur
due to the growth of parametric instabilities. Rocket and satellite
observations have provided evidence of nonlinear wave interactions in the
solar system, in particular, in relation to the generation and propagation of
radio waves in solar corona, interplanetary medium and Earth's
magnetosphere. These radio waves represent the electromagnetic signature of
solar-terrestrial coupling and are useful for monitoring the
space weather.
Nonlinear wave-wave coupling in plasmas can
be modelled as a dynamical system of coupled oscillators involving one, two or
higher-order wave triplets. For a three-wave dissipative system, the transition
from order to chaos may evolve via period doubling or intermittence. For a
two coupled three-wave Hamiltonian system, the transition may evolve via
the route of quasiperiodicity. We show that chaos in a dissipative three-wave
system can be controlled by applying a small sinusoidal wave to the system.
References
Chian A C-L 1999 Order and chaos in nonlinear wave interactions in
astrophysical and space plasmas, Plasma Phys. Contr. Fusion 41,
A437.
Chian A C-L, Lopes S R and Alves M V 1994 Generation of auroral
whistler-mode radiation via nonlinear coupling of Langmuir waves and
Alfvén waves, Astron. Astrophys. 290, L13.
Chian A C-L, Lopes S R and Abalde J R 1996, Hamiltonian chaos in two coupled
three-wave parametric interactions with quadratic nonlinearity, Physica D
99, 269.
Chian A C-L, Abalde J R, Alves M V and Lopes J R 1997, Coherent generation of
narrow-band circularly polarized radio bursts from the sun and flare
stars, Solar Phys. 173, 199.
Chian A C-L, Borotto F A and Gonzalez W D 1998, Alfvén intermittent
turbulence driven by temporal chaos, Astrophys. J. 505, 993.
Chian A C-L and Abalde J R 1999, Nonlinear coupling of Langmuir waves with
whistler waves in the solar wind, Solar Phys. 184, 403.
Chian A C-L, Borotto, F A, Lopes S R and Abalde J R 1999, Chaotic dynamics of
nonthermal planetary radio emissions, Planetary Space Sci., in press.
Lopes S R and Chian A C-L 1996, Controlling chaos in nonlinear
three-wave coupling, Phys. Rev. E 54, 170.
Lopes S R and Rizzato F B 1998, Chaos and energy redistribution in the
nonlinear interaction of two spatio-temporal wave triplets,
Physica D 117, 13.
Pakter R, Lopes S R and Viana R L 1997, Transition to chaos in the
conservative four-wave parametric interactions, Physica D 110, 277.
Robust spatiotemporal phenomena in one space dimension (I)
Pierre Coullet
Institut Non-Linéaire de Nice, Sophia-Antipolis, France
We review some of the robust instabilities which are observed in one
dimensional dissipative systems. More particularly, this lecture is
devoted to the instabilities which are induced by the continuous spatial
coupling of local dynamical systems.
The first of these instabilities was discovered by A.Turing in 1952. It
occurs already in two components reaction diffusion models when the
diffusion of the two species are very different. The singular nature of
this instability will be discussed. We will show in particular that
close to a particular bifurcation (Bogdanov-Takens codimension two
bifurcation) of the homogeneous reaction system, the instability can
occur with almost equal diffusion constant.
The Benjamin-Feir-Kuramoto-Newell instability will then be considered.
This "phase" instability of spatially coupled limit cycles will be
described geometrically.
We eventually discuss the question of the synchronization of coupled
limit cycles close to a homoclinic bifurcation. It will be shown that,
generically an instability always occurs in the vicinity of a homoclinic
bifurcation destroying the synchronization of the individual
oscillators. The nature of the instability depends on the nature of the
local dynamical system and the coupling considered. It can be either a
Benjamin-Feir-Kuramoto-Newell instability or a new amplitude instability
characterized by a period doubling which occurs at a finite wave-number.
A complete study of this new instability will be given.
The aim of this lecture is to give a qualitative approach to the
phenomena by using their normal form description. Interactive
simulations will be used during the lecture in order to illustrate these
phenomena. Examples from mechanics, chemistry, optics will be
considered.
References
Turing, A.N. Trans. Roy. Soc. Lond. B 237, 37
(1952).
J. Guckenheimer, P. Holmes, Nonlinear Oscillations, Dynamical Systems
and Bifurcation of Vector Fields. Appl .Math. Sci. 41 , Springer,
New-York (1983).
M. C. Cross and P. C. Hohenberg, Rev. Mod. Phys.
65, number 3, part II, 1993.
T. B. Benjamin and J. E. Feir, J. Fluid. Mech.
27, 241, 1967.
Y. Kuramoto, "Chemical Oscillations, Waves, and Turbulence",
Springer-Verlag, Berlin, 1984.
A.A Andronov, and L. Pontyagin. Dokl. Akad. Nauk,
SSSR, 14, 247, (1937). See also A. A. Andronov and al,
Theory of Bifurcation of Dynamical Systems on the Plane, Israel Program
For
Sci. Trans. (1971)
M. Argentina, P. Coullet, Phys. Rev. E 56, 2359 (1997)
M. Argentina et P. Coullet, Physica A 257, 45 (1998)
M. Argenina, P. Coullet and E. Risler, "Homoclinic instabilities in
spatially extended systems", preprint INLN (1999)
Robust spatiotemporal phenomena in one space dimension (II)
Pierre Coullet
Institut Non-Linéaire de Nice, Sophia-Antipolis, France
This second lecture is devoted to the description of localised
structures which occur in one-dimensional dissipative systems.
In the first part of the talk we study the propagative localised
structures known as excitable waves. Using the language of dynamical
system, we will describe the collision of two pulses. Depending on the
parameters the pulses either cross each other or coalesce. We show that
this phenomenon is actually a global bifurcation for the partial
differential equation. This bifurcation will be analyzed in the frame of
the geometrical theory of dynamical systems. This example provides a
unique case where the qualitative dynamical system theory have been used
to understand a phenomenon which cannot be understood in the frame of a
low dimensional dynamical system.
Static localised structures which can be observed in dissipative
one-dimensional systems have received recently a great deal of
attention. In the context of optics in particular they have been
considered as good candidates for building storage devices.
The question of the existence, the stability and the bifurcations of
these static localized structures will be related to the bistability
between a stable homogeneous state and a spatially periodic one. We will
show that the existence of a persistent front between a homogeneous
solution and a static periodic pattern is actually a consequence of the
transversality of heteroclinic orbits connecting a fixed point and a
limit cycle in reversible dynamical systems. This transversality
property implies the existence and the stability of localised solutions.
It also gives indications on the nature of the bifurcations of those
objects.
Examples from Optics and Chemistry will be considered. Interactive
numerical simulations will be presented during the talk in order to give an
intuition of the phenomena described.
References
M. Argentina, P. Coullet and L. Mahadevan, Phys. Rev. Lett.
79, 2803, (1997).
M. Argentina, P. Coullet and V. Krinsky, ''Crossing of excitable waves
in the
Fizu-Nagumo model'', preprint (1998), submitted to Trans. Phil.
Soc.
W. J. Firth and A. J. Scroggie, Phys. Rev. Lett., 76,
1623, (1996).
Y. Pomeau, Physica D 23, 3, (1985).
C. Riera, P. Coullet and C. Tresser, "Localised structures in one space
dimension", preprint INLN (1999)
Chaos and what to do about it: An overview
Predrag Cvitanovic
Physics & Astronomy, Northwestern Univ.,
Evanston, IL USA
and Niels Bohr Institute, Copenhagen, Denmark
That deterministic dynamics leads to chaos is no surprise to
anyone who has tried pool, billiards or snooker - that is what the game
is about - so we start our
course about what is chaos and what to do about it by a game of pinball.
This might seem a trifle trivial, but a pinball is to chaotic dynamics
what a pendulum is to integrable systems:
thinking clearly about what
is ``chaos'' in a pinball will help us tackle more difficult problems, such
as computing diffusion constants in deterministic gases, or
computing the Helium spectrum.
We all have an intuitive feeling for what a pinball does as it bounces
between the pinball machine disks, and only highschool level
Euclidean geometry is needed to describe the trajectory.
Turning this intuition into calculation will lead us,
in clear physically motivated steps, to almost everything one
needs to know about deterministic chaos:
from unstable dynamical flows, Poincaré sections,
Smale horseshoes, symbolic dynamics, pruning,
discrete symmetries, periodic orbits,
averaging over chaotic sets, evolution operators,
dynamical zeta functions, Fredholm determinants,
cycle expansions, quantum trace formulas and zeta functions,
and to the semiclassical quantization of helium.
Reference
Read chapter 1 and appendix A of
P. Cvitanovic, R. Artuso, R. Mainieri, G. Vattay et al.,
Classical and Quantum Chaos,
http://www.nbi.dk/ChaosBook/.
Dynamics, qualitative
Predrag Cvitanovic
Physics & Astronomy, Northwestern Univ.,
Evanston, IL USA
and Niels Bohr Institute, Copenhagen, Denmark
Confronted with a potentially chaotic dynamical system,
we analyze it through a sequence of three distinct stages; diagnose,
count, measure. First, we
determine the intrinsic dimension of the system - the minimum number of
degrees of freedom necessary to capture its essential dynamics.
If the system is
very turbulent (its attractor is of high dimension) we are, at present, out
of luck. We know only how to deal with the transitional regime between
regular motions and weak turbulence. In this regime the chaotic dynamics
is restricted to a space of
low dimension, the number of relevant parameters is small, and we can
proceed to the second step; we count and classify
all possible topologically distinct trajectories of the system.
If successful, we can proceed with the third step: investigate
the weights of the different pieces of the system.
In this lecture qualitative
dynamics of simple stretching and mixing flows is used to introduce Smale
horseshoes and symbolic dynamics, and
the topological dynamics is encoded by means of transition
matrices/Markov graphs.
We learn how to count and describe itineraries.
While computing the topological entropy
from transition matrices/Markov graphs, we encounter
our first zeta function.
By now we have covered for the first time the whole distance from diagnosing chaotic dynamics to
computing zeta functions. Historically, these topological zeta functions were the inspiration for
injecting statistical mechanics into computation of dynamical averages; Ruelle's
zeta functions are a
weighted generalization of the counting zeta functions.
Reference
Read chapters 2 and 3 of
P. Cvitanovic, R. Artuso, R. Mainieri, G. Vattay et al.,
Classical and Quantum Chaos,
http://www.nbi.dk/ChaosBook/.
Global dynamics
Predrag Cvitanovic
Physics & Astronomy, Northwestern Univ.,
Evanston, IL USA
and Niels Bohr Institute, Copenhagen, Denmark
This lecture is the core of the course:
we discuss the necessity of studying the averages of
observables in chaotic dynamics, and cast the formulas for averages
in a multiplicative form that motivates the introduction of
evolution operators.
In chaotic dynamics detailed prediction is impossible, as any finitely specified initial condition, no
matter how precise, will fill out the entire accessible phase space (similarly finitely grained) in finite
time. Hence for chaotic dynamics one does not attempt to follow individual trajectories to
asymptotic times; what is possible (and sensible) is description of the geometry of the set of
possible outcomes, and evaluation of the asymptotic time averages. Examples of such averages are
transport coefficients for chaotic dynamical flows, such as the escape rate, mean drift and the
diffusion rate; power spectra; and a host of mathematical constructs such as the generalized
dimensions, Lyapunov exponents and the Kolmogorov entropy. We shall now set up the formalism
for evaluating such averages within the framework of the periodic orbit theory. The key idea is to
replace the expectation values of observables by the expectation values of generating functionals.
This associates an evolution operator with a given observable, and leads to formulas for its
dynamical averages.
If there is one idea that you should learn about dynamics, it happens in this
lecture(s) and it is this: there is a fundamental local - global duality which
says that (global) eigenstates are dual to the (local) periodic geodesics. For
dynamics on the circle, this is called Fourier analysis; for dynamics on
well-tiled manifolds this is called Selberg trace formulas and zeta functions;
and for generic nonlinear dynamical systems the duality is embodied in trace
formulas, zeta functions and spectral determinants that we will now
introduce. These objects are to dynamics what partition functions are to
statistical mechanics. The bold claim is that once you understand this,
classical ergodicity, wave mechanics and stochastic mechanics are but
special cases, to be worked out at your leisure.
The strategy is this: Global averages such as escape rates can be extracted
from the eigenvalues of evolution operators. The eigenvalues are given by
the zeros of appropriate determinants. One way to evaluate determinants is
to expand them in terms of traces, log det = tr log. The traces are evaluated
as integrals over Dirac delta functions, and in this way the spectra of
evolution operators become related to periodic orbits.
The rest of the course is making sense out of this objects and learning how
to apply them to evaluation of physically measurable properties of chaotic
dynamical systems.
Reference
Read chapters 7, 8 and 9 of
P. Cvitanovic, R. Artuso, R. Mainieri, G. Vattay et al.,
Classical and Quantum Chaos,
http://www.nbi.dk/ChaosBook/.
Cycle expansions:
Semiclassical quantum mechanics
Predrag Cvitanovic
Physics & Astronomy, Northwestern Univ.,
Evanston, IL USA
and Niels Bohr Institute, Copenhagen, Denmark
In last lecture we have derived a plethora of periodic orbit trace
formulas, spectral determinants and zeta functions. Now we learn how to
expand these as cycle expansions, series ordered by increasing
topological cycle length, and evaluate average quantities like escape rates.
These formulas are exact, and, when the winds are kind, highly convergent.
The pleasant surprise is that the terms in such expansions fall off
exponentially or even faster, so that a handful of shortest orbits suffices for
rather accurate estimates of asymptotic averages.
The course now shifts gear to
recent advances in the periodic orbit theory of chaotic, non-integrable
systems, and the modern generalization of the De Broglie - Bohr quantization
of hydrogen atom.
Instead of quantizing by suspending standing-wave configurations
on stable Keplerian orbits, one suspends the standing-wave configurations
on the infinity of unstable orbits. Such unstable periodic orbits are observed
experimentally in the helium atom, the hydrogen in strong external fields,
and other systems.
This is what could have been done with the old quantum mechanics if
physicists of 1910's were as familiar with chaos as you by now are.
The Gutzwiller trace formula together with the
corresponding spectral determinant, the
central results of the semiclassical periodic orbit theory, are derived.
The helium atom spectrum can then be computed via spectral determinants.
Reference
Read chapters 9, 15 and 17 of
P. Cvitanovic, R. Artuso, R. Mainieri, G. Vattay et al.,
Classical and Quantum Chaos,
http://www.nbi.dk/ChaosBook/.
Trace formulas for stochastic evolution operators
Predrag Cvitanovic
Physics & Astronomy, Northwestern Univ.,
Evanston, IL USA
and Niels Bohr Institute, Copenhagen, Denmark
Intuitively, the noise inherent in any realistic system washes out
fine details and makes chaotic averages more robust. Quantum mechanical
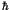 resolution of phase space implies that in semi-classical approaches
no orbits longer than the Heisenberg time need be taken into account.
We explore these ideas in some detail by casting stochastic dynamics
into path integral form and developing perturbative and nonperturbative
methods for evaluating such integrals. In the weak noise case the
standard perturbation theory is expansion in terms of Feynman diagrams.
Now the surprise; we can compute the same corrections faster and to a
higher order in perturbation theory by integrating over the neighborhood
of a given saddlepoint exactly by means of a nonlinear change of
field variables. The new perturbative expansion appears more compact
than the standard Feynman diagram perturbation theory; whether it is
better than traditional loop expansions for computing field-theoretic
saddlepoint expansions remains to be seen, but for a simple system we study
the result is a stochastic analog of the Gutzwiller trace formula
with the
resolution of phase space implies that in semi-classical approaches
no orbits longer than the Heisenberg time need be taken into account.
We explore these ideas in some detail by casting stochastic dynamics
into path integral form and developing perturbative and nonperturbative
methods for evaluating such integrals. In the weak noise case the
standard perturbation theory is expansion in terms of Feynman diagrams.
Now the surprise; we can compute the same corrections faster and to a
higher order in perturbation theory by integrating over the neighborhood
of a given saddlepoint exactly by means of a nonlinear change of
field variables. The new perturbative expansion appears more compact
than the standard Feynman diagram perturbation theory; whether it is
better than traditional loop expansions for computing field-theoretic
saddlepoint expansions remains to be seen, but for a simple system we study
the result is a stochastic analog of the Gutzwiller trace formula
with the 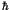 corrections so far computed to five orders higher than
what has been attainable in the quantum-mechanical applications.
corrections so far computed to five orders higher than
what has been attainable in the quantum-mechanical applications.
Resume
A motion on a strange attractor can be approximated by
shadowing the orbit by a sequence of nearby periodic orbits of finite
length. This notion is here made precise by approximating orbits by
primitive cycles, and evaluating associated curvatures. A curvature
measures the deviation of a longer cycle from its approximation by shorter
cycles; the smoothness of the dynamical system implies exponential
(or faster) fall-off for (almost) all curvatures.
The technical prerequisite for implementing
this shadowing is a good understanding of the symbolic
dynamics of the classical dynamical system.
The resulting cycle expansions offer an
efficient method for evaluating classical and
quantum periodic orbit sums; accurate estimates can be obtained by
using as input the lengths and eigenvalues of
a few prime cycles.
To keep exposition simple we have here illustrated the utility of cycles
and their curvatures by a pinball game.
Glancing back, we see that the formalism is very general, and
should work for any average over any chaotic set which satisfies
two conditions:
1. the weight associated with the observable under
consideration is multiplicative along the trajectory;
2. the set is organized in such a way that the nearby points
in the symbolic dynamics have nearby weights.
Reference
Read chapter 22 and the
take-home problem set for the next millennium in
P. Cvitanovic, R. Artuso, R. Mainieri, G. Vattay et al.,
Classical and Quantum Chaos,
http://www.nbi.dk/ChaosBook/.
Semiclassical matrix elements and cross sections
Bruno Eckhardt
Fachbereich Physik, Philipps Universität Marburg,
Germany
The semiclassical trace formula of Gutzwiller can be extended
to include diagonal matrix elements. With this it becomes possible
to describe cross sections, e.g. for excitations of molecules.
In the lectures I will discuss how this can be used to
describe both universal features which otherwise could
be discussed within random matrix theory and non-universal
features connected with classical periodic orbits and their
bifurcations.
Lecture 1:
Transitions in molecules are described by Franck-Condon
factors, which are matrix elements between eigenstates
of an operator and projectors on the initial state.
In order to calculate them within periodic orbit theory
the Gutzwiller trace formula has to be extended.
For operators which are smooth in the classical limit
this is easy, but for singular ones like projection
operators higher order corrections have to be taken into
account. This extension is particularly easy to achieve
in the time domain, both for the calculation of
the smooth average part and for the contributions
from periodic orbits.
Given this expression for the matrix element weighted
density of states one can now turn to a calculation of
the correlation function or, more generally, the two point
form factor. One of the aims of the lecture will be to
describe how the random matrix results of Alhassid and
Fyodorov can be obtained.
Lecture 2:
One of the distinguishing features of semiclassical
periodic orbit theory is its potential to describe
non-universal properties, specific to the system in
question and beyond the reach of random matrix theory.
The most prominent effects arise in the neighborhood
of bifurcations where the semiclassical amplitudes
diverge. Catastrophe theory can be used to calculate
uniformized amplitudes (as shown in a number of
recent works). The lecture will focus on two
aspects of our work:
i) In order to analyze the collective effects of
many bifurcations we have studied
the statistical behaviour in the standard map
as a function of the control parameter 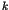 .
This contributes to our understanding of the
importance of bifurcations in long periodic orbits.
.
This contributes to our understanding of the
importance of bifurcations in long periodic orbits.
ii) The divergent classical weights have a pronounced effect
also on wave functions. One measure of localization in
wave functions is the inverse participation ratio.
In particular, for saddle node bifurcations, we find
prelocalized states below the bifurcation and oscillations
in the inverse participation ratio above the bifurcation.
The oscillations can be described by Airy functions,
which can be motivated (but not fully justified)
by the semiclassical matrix element theory discussed in
lecture 1.
References
B. Eckhardt, S. Fishman, K. Müller and D. Wintgen,
Phys. Rev. A 45, (1992) 3531-3539
B. Eckhardt, O. Agam, S. Fishman, J. Keating, J. Main und K. Müller
Phys. Rev. E 52, (1995) 5893-5903
B. Eckhardt and J. Main, Phys. Rev. Lett. 75, (1995) 2300-2303
B. Eckhardt, Physica D 109, (1997) 53-58
B. Hüpper and B. Eckhardt, Phys. Rev. A 57, (1998) 1536-1547
Chaotic Huygens phenomenon
and on-off intermittency
Hirokazu Fujisaka
Department of Applied Analysis and Complex Dynamical Systems,
Graduate School of Informatics, Kyoto University,
Japan
Intermittency phenomena is quite ubiquitous in nonlinear dynamics. The most
famous one is observed in fluid turbulence. Nowadays it is
believed that the intermittency is one of key concepts for characterization
or
analyzing various phenomena in nonlinear dynamical systems. The most
familiar one is the Pomeau-Manneville intermittency, which is observed when
a periodic motion is either destroyed or undergoes the instability when an
external control parameter is changed. On the other hand, when a particular
chaotic motion undergoes an instability, an intermittency with statistical
characteristics different from that of PM comes to appear. This is called
the
modulational intermittency or
on-off intermittency. In particular, under certain condition two identical
chaotic oscillators synchronize, (chaotic Huygens phenomenon). When the
synchronization becomes unstable, we typically observe the on-off
intermittency, (Fujisaka-Yamada 1985).
On-off intermittency is one of typical evolutions in nonlinear dynamics.
In the present lecture, I will give several different mathematical
models with both small and large number of degrees of freedom and also discuss
physical system. Then I will review general criteria on the observability of
on-off intermittency and give statistical laws. Introducing a stochastic
model, I will show that these statistical laws can be derived.
Furthermore the possibility of the construction of solvable models of on-off
intermittency will be addressed.
References
Fujisaka H and Yamada T 1985 Prog. Theor. Phys. 74 918
Fujisaka H and Yamada T 1986 Prog. Theor. Phys. 75 1087
Fujisaka H and Yamada T 1983 Prog. Theor. Phys. 69 32
Yamada T and Fujisaka H 1983 Prog. Theor. Phys. 70 1240
Platt N, Spiegel E.-A. and Tresser C 1993 Phys. Rev. Lett. 70
279
Heagy J.-F., Platt N and Hammel S.-M. 1994 Phys. Rev. E 49 1140
Ott E and Sommerer J.-C. 1994 Phys. Lett. A 188 39
Lai Y.-C. and Grebogi C 1995 Phys. Rev. E 52 R3313
Harada T, Hata H and Fujisaka H 1999 J. Phys. A 32
Fujisaka H, Matsushita S and Yamada T 1997 J. Phys. A 30 5697
Fujisaka H, Ouchi K, Hata H, Masaoka B and Miyazaki S 1998 Physica D
114 237
Yamada T, Fukushima K and Yazaki T 1989 Prog. Theor. Phys.
Suppl. No.99 120
Cenys A, Namajunas A, Tamserius A and Schneider T 1996 Phys. Lett. A
213 259
Rodelsperger F, Cenys A and Benner H 1995 Phys. Rev. Lett. 75
2594
Yamada T and Fujisaka H 1986 Prog. Theor. Phys. 76 582
Hata H and Miyazaki S 1997 Phys. Rev. E 55 5311
Miyazaki S and Hata H 1998 Phys. Rev. E 58 7172
``Thermodynamics" approach
to on-off intermittency
Hirokazu Fujisaka
Department of Applied Analysis and Complex Dynamical Systems,
Graduate School of Informatics, Kyoto University, Japan
Large deviation theory (LDT) in the probability theory is the
straightforward extension of the
central limit theorem which has played a very important role in statistical
mechanics. Since LDT addresses the large fluctuations observed in
nonlinear dynamics, typically for intermittency dynamics, it is natural to
expect that LDT can also be a powerful theoretical framework to analyze
chaotic dynamics.
In the lecture I first review LDT from the physicist point of view, and
discuss how the statistical quantities characterizing LDT are determined
both experimentally and theoretically. Then I will apply the LDT
approach to examples in both chaotic and stochastic systems including
the stochastic model of on-off intermittency. It is shown that the LDT
analysis yields many different aspects of fluctuations which cannot be
captured by
the traditional statistical analysis based on two-time correction functions.
The short time dynamics of on-off intermittency shows a characteristic
quite different from the long time dynamics which can be discussed
within LDT. To analyze it, we introduce the concept of
a self-similar dynamics for on-off fluctuations. Although the conventional
LDT cannot be applied for such short time dynamics, I will show that
LDT is ``again" applicable.
References
Fujisaka H and Inoue M 1987 Prog. Theor. Phys. 77 1334
Fujisaka H and Shibata H 1991 Prog. Theor. Phys. 85 187
Fujisaka H 1992 in From Phase Transitions to Chaos eds. G Györgyi
et al (Singapore: World Scientific) pp 34-48
Beck C and Schlögl F 1993 Thermodynamics of Chaotic Systems - An
Introduction - (Cambridge: Cambridge University Press)
Ott E 1993 Chaos in Dynamical Systems (Cambridge: Cambridge University
Press)
Fujisaka H and Yamada T 1985 Prog. Theor. Phys. 74 918
Fujisaka H and Yamada T 1986 Prog. Theor. Phys. 75 1087
Platt N, Spiegel E.-A. and Tresser C 1993 Phys. Rev. Lett. 70
279
Heagy J.-F., Platt N and Hammel S.-M. 1994 Phys. Rev. E 49 1140
Ott E and Sommerer J.-C. 1994 Phys. Lett. A 188 39
Lai Y.-C. and Grebogi C 1995 Phys. Rev. E 52 R3313
Yamada T and Fujisaka H 1986 Prog. Theor. Phys. 76 582
Yamada T and Fujisaka H 1990 Prog. Theor. Phys. 84 824
Fujisaka H and Yamada T 1993 Prog. Theor. Phys. 90 529
Miyazaki S and Hata H 1998 Phys. Rev. E 58 7172
Fujisaka H and Yamada T 1987 Prog. Theor. Phys. 77 1045
The chaotic hypothesis: a review and some applications
Giovanni Gallavotti
Fisica, Universitá di Roma, Rome, Italia
The chaotic hypothesis is a reformulation of a principle stated by
Ruelle in the early '70s (1973). It is a principle of very ambitious
nature as it is a proposal for the extension of the ergodic hypothesis
to nonequilibrium statistical mechanics systems. The entropy creation
rate in a thermostated system by thermostats of mechanical nature, in
which the energy cannot grow in spite of nonconservative external
forces acting on the system, is identified with the divergence of the
equations of motion. The fluctuations of the latter obey a universal
relation: the fluctuation theorem. Further more heuristic
developments of the chaotic hypothesis suggest introducing the notion
of nonequilibrium ensembles: they offer the new idea that in systems
out of equilibrium it can happen that the equations of motion
themselves may become ``parameters'' of the nonequilibrium
ensembles. And systems obeying different equations of motions may be
equivalent in a sense analogous to the equivalence of the canonical
and microcanonical ensembles, for instance. Similar ideas can be
discussed in the theory of developed turbulence, which is the field in
which the original ideas of Ruelle were developed.
References
Bonetto, F., Gallavotti, G.: Reversibility,
coarse graining and the chaoticity principle, Communications in
Mathematical Physics, 189, 263-276, 1997.
Bonetto, F., Gallavotti, G., Garrido, P.: Chaotic
principle: an experimental test, Physica D, 105, 226-252,
1997.
Bonetto, F., Gallavotti, G., Garrido, P.:
Chaotic principle: an experimental test, Physica D, 105,
226-252, 1997.
Gallavotti, G.: Some rigorous results about
3D Navier Stokes, in "Turbulence in spatially extended systems", p.45-
74, ed. R. Benzi, C. Basdevant, S. Ciliberto, Nova Science Publishers,
Commack (NY), 1993.
Gallavotti, G.: Ergodicity, ensembles,
irreversibility in Boltzmann and beyond, Journal of Statistical
Physics. 78, 1571-1589, 1995.
Gallavotti, G.: Extension of Onsager's
reciprocity to large fields and the chaotic hypothesis,
Physical Review Letters, 77, 4334-4337, 1996.
Gallavotti, G.: New methods in nonequilibrium gases and
fluids, Proceedings of the conference Let's face chaos through
nonlinear dynamics, U. of Maribor, 24 june- 5 july 1996,
ed. M. Robnik, in print in Open Systems and Information Dynamics,
Vol. 6, 1999.
Gallavotti, G., Ruelle, D.: SRB states and nonequilibrium
statistical mechanics close to equilibrium, Communications in
Mathematical Physics, 190, 279-285, 1997.
Gallavotti, G.: Dynamical ensembles equivalence
in fluid mechanics, Physica D, 105, 163-184, 1997.
Gallavotti, G.: Chaotic hypothesis: Onsager reciprocity and
fluctuation-dissipation theorem,
Journal of Statistical Phys., 84, 899-926, 1996.
Gallavotti, G.:
Equivalence of dynamical ensembles and Navier Stokes equations,
Physics Letters, 223, 91-95, 1996.
Gallavotti, G.: SRB states and nonequilibrium statistical
mechanics close to equilibrium, Communications in Mathematical Physics,
190, 279-285, 1997 (D. Ruelle)
Gallavotti, G.: Ipotesi per una introduzione alla Meccanica
dei Fluidi, ``Quaderni del CNR-GNFM'', vol. 52, p. 1-428,
Firenze, 1997.
Gallavotti, G.: Chaotic principle: some
applications to developed turbulence, Journal of Statistical Physics,
86, 907-934, 1997.
Gallavotti, G.: Reversible Anosov maps and
large deviations, Mathematical Physics Electronic Journal, MPEJ,
(http:// mpej.unige.ch), 1, 1-12, 1995.
Gallavotti, G.: Breakdown and regeneration of time reversal
symmetry in nonequilibrium Statistical Mechanics, Physica D, 112,
250-257, 1998.
Gallavotti, G., Cohen, E.G.D: Dynamical
ensembles in nonequilibrium statistical mechanics, Physical Review
Letters, 74, 2694-2697, 1995.
Gallavotti, G., Cohen, E.G.D: Dynamical
ensembles in stationary states, Journal of Statistical Physics,
80, 931-970, 1995.
Gallavotti, G.: Extension of Onsager's
reciprocity to large fields and the chaotic hypothesis,
Physical Review Letters, 77, 4334-4337, 1996.
Cohen, E.G.D., Gallavotti, G.: Note on Two Theorems in
Nonequilibrium Statistical Mechanics, mp_arc 99-88, cond-mat
9903418.
Gallavotti, G.: Fluctuation patterns and conditional
reversibility in
nonequilibrium systems, in print on Annales de l' Institut
H. Toincaré, mp_arc at math. utexas. edu #97-124, chao-dyn at
xyz. lanl. gov #9703007.
Gallavotti, G.:
Mécanique statistique hors équilibre: l'héritage
de Boltzmann, mp_arc at math. utexas. edu: # 98-54,
chao-dyn at xxx. lanl. gov: chao-dyn/9802012.
Gallavotti, G.: Breakdown and regeneration of time reversal
symmetry in nonequilibrium Statistical Mechanics, Physica D, 112,
250-257, 1998.
Gallavotti, G.: Chaotic dynamics, fluctuations,
non-equilibrium ensembles, Chaos, 8, 384-392, 1998.
Gallavotti, G.: A local fluctuation theorem, Physica A,
qq 263, 39-50, 1999.
Gallavotti, G.: Chaotic Hypothesis and Universal Large Deviations
Properties, Documenta Mathematica, extra volume ICM98, vol. I,
p. 205-233, 1998, also in chao-dyn 9808004.
Gallavotti, G.: Trattatello di Meccanica Statistica,
``Quaderni del CNR-GNFM'', vol. 50, p. 1-350, Firenze, 1995.
English version available on http://ipparco.roma1.infn.it.
Gallavotti, G.: Ipotesi per una introduzione alla Meccanica
dei Fluidi, ``Quaderni del CNR-GNFM'', vol. 52, p. 1-428,
Firenze, 1997.
Most of the papers (and books) can be freely downloaded from:
http://ipparco.roma1.infn.it
e-mail: giovanni at ipparco.roma1.infn.it
Quantum diffusion and fractal spectra
T. Geisel and R. Ketzmerick
Max-Planck-Institut für Strömungsforschung, Göttingen,
and Fakultät Physik, Universität Göttingen,
Germany
While in the past the influence of classical chaos on quantum spectra was investigated
intensely in the case of discrete spectra, the cases of uncountable and in particular
fractal spectra have received attention only recently. We show that the latter are
associated with specific dynamical properties:
(i) They generate unbounded quantum
mechanical diffusion processes in contrast to the dynamical localization known from
the kicked rotator and other systems, and
(ii) cause an algebraic decay of correlations
as a function of time. We show that these properties are governed by generalized
dimensions 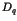 of the spectrum and eigenfunctions.
of the spectrum and eigenfunctions.
In particular, the asymptotic decay of correlations is determined by the dimension 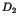 of
the spectral measure, while the diffusive spreading of wave packets is related to the
ratio of the dimensions
of
the spectral measure, while the diffusive spreading of wave packets is related to the
ratio of the dimensions 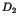 of the spectral measure and of the eigenfunctions,
respectively.
Such fractal spectra show up for Bloch electrons in magnetic fields, in particular in
artificial superlattices of quantum dots and antidots on semiconductor heterojunctions
(electronic Sinai billiards). Quantum mechanical descriptions based on Harper's equation
lead to a fractal spectrum known as Hofstadter's butterfly. This model has an integrable
classical limit, however, and thus fails in these superlattices, where chaotic trajectories
prevail. More realistic models that allow for chaos in the classical limit exhibit
peculiar metal-insulator transitions and transitions between absolutely continuous and pure
point spectra induced by classical chaos. We show that they can be understood in terms of
avoided band crossings.
of the spectral measure and of the eigenfunctions,
respectively.
Such fractal spectra show up for Bloch electrons in magnetic fields, in particular in
artificial superlattices of quantum dots and antidots on semiconductor heterojunctions
(electronic Sinai billiards). Quantum mechanical descriptions based on Harper's equation
lead to a fractal spectrum known as Hofstadter's butterfly. This model has an integrable
classical limit, however, and thus fails in these superlattices, where chaotic trajectories
prevail. More realistic models that allow for chaos in the classical limit exhibit
peculiar metal-insulator transitions and transitions between absolutely continuous and pure
point spectra induced by classical chaos. We show that they can be understood in terms of
avoided band crossings.
References
T. Geisel, R. Ketzmerick, G.Petschel, in Quantum Chaos -
Between Order and Disorder,
eds. G. Casati and B. V. Chirikov (Cambridge University Press, Cambridge 1995) p. 633.
R. Ketzmerick, K. Kruse, S. Kraut, T. Geisel, Phys. Rev. Lett., 79, 1959 (1997).
R. Ketzmerick, K. Kruse, T. Geisel, Phys. Rev. Lett., 80, 137 (1998).
Pattern formation in the developing visual cortex
T. Geisel and F. Wolf
Max-Planck-Institut für Strömungsforschung, Göttingen,
and Fakultät Physik, Universität Göttingen,
Germany
Nonlinear dynamics appears to play a role not only in chaos and faces but also in the
information
processing in brains and the development of brains. Visual and other external information is
often represented
in the cortex in the form of neural maps (e.g. retinal space or ocularity into
cortical space),
which exhibit characteristic patterns varying from species to species. These maps are
known in great detail from neurobiological studies which employ high resolution
techniques e.g.
like optical imaging. Some of the best studied examples are the orientation preference
maps,
cortical neurons exhibiting different preferred orientations of visual stimuli.
It has long been hypothesized that the orientation selectivity of single neurons and
the spatial pattern of orientation preferences in primary visual cortex arise due to
activity-dependent
self-organization of neuronal circuitry during early life. We demonstrate the relevance
of nonlinear dynamics for the theoretical analysis of this self-organization process.
The talk will present theoretical work applied to recent experiments on strabismic and
normal cats and will address the following questions:
Which mechanisms control the formation of neural maps?
How does experience influence the patterns?
Does the cortex undergo a symmetry breaking bifurcation during development?
Can we explain the different pattern layout in different species from common principles?
References
H.-U. Bauer, T. Geisel, K. Pawelzik, F. Wolf, in From Statistical Physics to Statistical Inference and Back,
eds. J.-P. Nadal and P. Grassberger (Kluwer Academic Publ., 1994) p. 249.
H.-U. Bauer, T. Geisel, K. Pawelzik, F. Wolf,
Spektrum der Wissenschaft (1996), 4, 38.
F. Wolf, T. Geisel, Nature, 395, 73 (1998).
Resetting and entraining biological oscillators
Leon Glass
Department of Physiology,
McGill University, Montreal, Quebec, Canada
Biological oscillators are ubiquitous and underly many important
biological functions including the heartbeat, respiration, and
reproduction. Each of these rhythms is generated and regulated by
complex mechanisms and feedback. Despite the different mechanisms,
from a mathematical perspective, they might all be associated with a
stable limit cycle oscillations in an appropriate nonlinear equation.
Based on this assumption, it is possible to make a number of different
predictions concerning the effects of single and periodic stimuli
delivered to the oscillator (Winfree, 1980; Glass and Mackey, 1988).
The main results are: single stimuli might either advance or delay the
onset of the next oscillation depending on the amplitude and phase of
the stimulus; plots of the resetting functions as a function of the
phase of the stimuli fall into distinct classes which can be
classified based on continuity considerations; and if the limit cycle
is strongly attracting, then based on the analysis of the effects of
single stimuli on the oscillations it is possible to predict the effects
of periodic stimuli
(Guevara and Glass, 1982; Keener and Glass, 1984). These theoretical
predictions have succeeded in helping to identify chaotic dynamics
during periodic stimulation delivered to spontaneously beating
aggregates of heart cells (Guevara, Glass, Shrier, 1981). I also
discuss the limitations of the above theory. In particular, if
relaxation to the limit cycle is not instantaneous, then the analysis
becomes much more difficult (Glass and Sun, 1994). Also the effects of
stimulation can change the properties of the limit cycle oscillator
(Kunysz, Glass, Shrier, 1995). Although the geometric approach I
describe in this and subsequent lectures is conceptually simple, there
are many subtleties. It is hard to appreciate these without doing
computations. Students who are particularly motivated by this topic,
would benefit by reading Chapters 6 and 7 in Glass and Mackey (1988)
prior to the summer school and attempting Problem 14(B) on p. 208. I
will treat anyone who makes a decent effort to a free beer (or
coffee)!
References
L. Glass, M.C. Mackey. From Clocks to Chaos: The
Rhythms of Life. (Princeton University Press, Princeton, 1988).
L. Glass, J. Sun. Periodic forcing of a limit cycle oscillator:
Fixed points, Arnold tongues, and the global organization of
bifurcations. Physical Review E 50, 5077-5084 (1994).
M.R. Guevera, L. Glass. Phase-locking, period-doubling
bifurcations and chaos in a mathematical model of a
periodically driven biological oscillator: A theory for the
entrainment of biological oscillators and the generation of
cardiac dysrhythmias. Journal of Mathematical Biology
14, l-23 (1982).
M.R. Guevera, L. Glass, A. Shrier. Phase-locking, period-doubling
bifurcations and irregular dynamics in periodically stimulated
cardiac cells. Science 214, 1350-1353 (1981).
J. Keener, L. Glass. Global
bifurcations of a periodically forced nonlinear
oscillator. Journal of Mathematical Biology 21,
175-190 (1984).
A. Kunysz, L. Glass, A. Shrier. Overdrive suppression of
spontaneously beating chick heart cell aggregates: Experiment and
theory. American Journal of Physiology 269 (Heart,
Circulatory Physiology 38), H1153-H1164 (1995).
A. T. Winfree The Geometry of Biological Time (Springer-Verlag,
New York, 1980).
Dynamics of cardiac arrhythmias
Leon Glass
Department of Physiology,
McGill University, Montreal, Quebec, Canada
Cardiac arrhythmias are abnormal cardiac rhythms in which there is
abnormal impulse generation, abnormal conduction of excitation, or
both. Since the heart is a nonlinear system, the classifications of
cardiac arrhythmias (by cardiologists) should correspond to
classifications of bifurcations in nonlinear systems (by
mathematicians). This lecture introduces basic cardiac anatomy and
electrophysiology (Goldberger and Goldberger, 1994; Glass, 1996). Two
arrhythmias that have successfully been analyzed mathematically are
heart block, in which some of the excitations in the upper chambers of
the heart do not conduct successfully to the lower chambers of the
heart (Shrier et al., 1987) and parasystole, in which there is a
competition for control of the heart by two competing pacemakers
(Glass, Goldberger, Bélair, 1984; Bub and Glass, 1995). These two
arrhythmias are not particularly dangerous. However, there has also been
mathematical analysis of more dangerous arrhythmias such as
tachycardias, in which the heartbeat is abnormally fast. One
conceptual model of tachycardias is that the excitation is associated
with a pulse that circulates on a one-dimensional ring. Surprisingly,
this simple model leads to the following predictions: if the
circumference of the ring is too small, either reentry will be
impossible or there will be quasiperiodic fluctuations of cycle time
(Courtemanche, Glass, Keener, 1993); a single stimulus will either
annihilate or reset the rhythm (Glass and Josephson, 1995); the
effects of periodic stimulation can be computed based on the analysis
of the resetting induced by a single stimulus (Nomura and Glass,
1996). I will describe recent efforts to test these predictions
experimentally. Anyone wishing to prepare for this lecture should try
to analyze the following not so hypothetical situation. An electrode
is inserted into the right atrium of a patient's heart. The electrode
is controlled by a computer under your guidance. The electrode delivers
brief shocks that are capable of exciting the heart (this is the
principle of an artificial pacemaker). What different rhythms could
you elicit from the heart as you change the frequency and amplitude of
the stimulation?
References
G. Bub, L. Glass. Bifurcations in a discontinuous circle map: A theory for a
chaotic cardiac arrhythmia. International Journal of Bifurcation
and Chaos 5, 359-371 (1995).
Courtemanche, L. Glass, J.P. Keener. Instabilities of
a propagating pulse in a ring of excitable media. Physical Review
Letters 70, 2182-2185 (1993).
L. Glass. Dynamics of cardiac arrhythmias. Physics Today
49 (Number 8, Part 1) 40-45 (1996).
L. Glass, A. Goldberger, J. Bélair. Dynamics of pure
parasystole. American Journal of Physiology 251
(Heart Circ. Physiol. 20), H841-H847 (1986).
L. Glass,
M.E. Josephson. Resetting and annihilation of reentrant abnormally
rapid heartbeat. Physical Review Letters 75, 2059-2063
(1995).
A. L. Goldberger, E. Goldberger Clinical Electrocardiology, Fifth
Edition (Mosby, St. Louis, 1994).
T. Nomura, L. Glass. Entrainment and termination of reentrant
wave propagation in a periodically stimulated ring of excitable
media. Physical Review E 53, 6353-6360 (1996).
A. Shrier,
H. Dubarsky, M. Rosengarten, M.R. Guevara, S. Nattel,
L. Glass. Prediction of complex atrioventricular conduction
rhythms in humans using the atrioventricular nodal recovery
curve. Circulation 76, 1196-1205 (1987).
Controlling cardiac arrhythmias
Leon Glass
Department of Physiology,
McGill University, Montreal, Quebec, Canada
A variety of different approaches have been devised to help control
cardiac arrhythmias. Therapeutic approaches to controlling cardiac
arrhythmias include drug therapy, electrical therapy such as
pacemakers or implantable defibrillators, and ablation in which a
portion of the heart is destroyed. To the best of my knowledge, none
of the therapies currently used have been developed based on a
mathematical analysis of nonlinear dynamics of cardiac arrhythmias.
This lecture further analyzes dynamics of arrhythmias and demonstrates
approaches to controlling arrhythmias in model systems using
mathematical analyses. The first part of the talk describes repetitive
paroxysmal tachycardias, in which there is an incessant starting and
stopping of arrhythmia (Parkinson and Papp, 1967), and experimental
models displaying similar dynamics. The experimental models are
generated by: stimulation of spontaneously oscillating cardiac cells
with a fixed delay after an activation (Kunysz, Shrier, Glass, 1997);
stimulation of the atria of rabbit hearts at a fixed delay after the
activation of the ventricles (Sun et al., 1995); and culturing heart
cells in a monolayer (Bub, Glass, Shrier, 1998). In all three
examples, the interactions between pacemakers, conduction and
``fatigue'' leads to bursting rhythms. I then describe mathematical
methods being developed to control cardiac arrhythmias. An early
example adopted methods of ``chaos'' control to an experimental model
system (Garfinkel et al., 1992) but see also (Glass and Zeng, 1994).
More recent work tunes the adjustable delay in a reentrant circuit to
control an alternating rhythm (Hall et al., 1997). Finally, analysis
of wave propagation might help cardiologists successfully locate areas
to target for ablation (Hall and Glass, 1999). In view of the
nonlinear nature of the heart, and the complex dynamics of cardiac
arrhythmias it seems inevitable that theoretical analyses based on
nonlinear dynamics will lead to successful new therapies, but we are
still awaiting the first demonstration.
References
G. Bub, L. Glass, A. Shrier. Bursting calcium rotors in cultured cardiac
myocyte monolayers. Proceedings of the National Academy of
Sciences (USA) 95, 10283-10287 (1998).
A. Garfinkel, M. L. Spano, W. L. Ditto, J.N. Weiss. Controlling
cardiac chaos. Science
257, 1230-1235 (1992).
L. Glass, W. Zeng. Bifurcations in flat-topped maps
and the control of cardiac chaos. International Journal of
Bifurcation and Chaos 4, 1061-1067 (1994).
K. Hall, L. Glass. Locating ectopic foci. Journal of
Cardiovascular Electrophysiology 10 387-398 (1999).
K. Hall, D. J. Christini, M. Tremblay, J. J. Collins, L. Glass,
J. Billette. Dynamic control of cardiac alternans. Physical
Review Letters 78, 4518-4521 (1997).
A. Kunysz, A. Shrier, L. Glass. Bursting behavior
during fixed delay stimulation of spontaneously beating chick heart
cell aggregates. American Journal of Physiology 273 (
Cell Physiology 42), C331-C346 (1997).
J. Parkinson, C. Papp. Repetitive paroxysmal tachycardia Br.
Heart J 9, 241-262 (1947).
J. Sun, F. Amellal,
L. Glass, J. Billette. Alternans and period-doubling bifurcations in
atrioventricular nodal conduction. Journal of Theoretical
Biology 173, 79-91 (1995).
Growth phenomena in cellular automata
Janko Gravner
Mathematics Department,
University of California, Davis
A cellular automaton (CA) is a spatially
distributed dynamical system which evolves via
local, homogeneous, parallel updating, which
may be deterministic or random.
Our focus will be on self-organization:
a tendency toward large-scale, coherent
structure from disordered initial states.
The examples will mostly feature irreversible
dynamics outside the scope of traditional
statistical mechanics, which we loosely call
growth models. We will mainly review development
of mathematical theory developed for several classes
of CA, but will also present insights gathered
from simulations and open problems.
In the first talk, we will start with the basic definitions and
a menagerie of illustrative examples.
We will present an analysis of additive CA,
discussing particularly replication and generation of
fractals. Another basic example is oriented
percolation, a prototype for a phase transition
and the fundamental building block in rescaling
arguments. A model for an excitable medium
will provide an example of locally periodic CA.
We will then briefly touch on
measures of complexity of CA rules and on
the most famous of all CA, the Game of Life.
The second talk will go into more depth on
the subject of nucleation and growth properties
of CA. The first subject will be shape theory
for monotone growth, reviewing Wulff construction
for deterministic and random CA. By contrast,
non-monotone cases can only be rigorously
handled when a recursive analysis is available.
We will
present some examples of recursive solidification
which lead to fractal growth and are extremely sensitive
to random perturbations. Next, we will
mention some growth models based
on random walks that generate isotropic shapes, and other,
much less tractable,
which yield random fractals.
Finally, we will review nucleation theory in both
supercritical and critical monotone CA. Specifically, we will
review power laws, density decays and last holes
problems, emergent shapes, and effects of
polluted environments. Time permitting, some
percolation effects in excitable media will
be discussed.
References
Aizenman M and Lebowitz J 1988 J. Phys. A: Math. Gen 21 3801.
Bramson M and Neuhauser C 1994 Annals of Probability 22 244.
Bramson M, Griffeath D, and Lawler G 1992 Annals of Probability
20 2117.
Chopard B and Droz M 1999 Cellular Automata Modeling
of Physical Systems. Cambridge University Press.
Fisch R, Gravner J, and Griffeath D 1993 Annals
of Applied Probability 3 935.
Gravner J 1999 Growth phenomena in cellular automata. Preprint.
Gravner J and Griffeath D 1996 Annals of Probability 24 1752.
Gravner J and Griffeath D 1998 Advances in Applied Mathematics 21
241.
Gravner J and Griffeath D 1998 Scaling laws for a class of critical
cellular automaton growth rules. Preprint.
Griffeath D 1994. In Probability and Phase Transition,
G. Grimmett, Editor, Kluwer, pg. 49.
Packard N and Wolfram S 1985 Journal of Statistical Physics
38 901.
Toffoli T and Margolus N 1987 Cellular Automata Machines.
MIT Press.
Vichniac G 1984 Physica D 10 96.
Willson S 1984 Discrete Appl. Math. 8 1991.
The onset of turbulence despite stable laminarity
Siegfried Grossmann
Fachbereich Physik der Philipps-Universität, Marburg, Germany
This lecture is devoted to the recent explanation of the mechanism
which determines the onset of turbulence in laminar shear flows. This
is different from the routes to turbulence characterized by a sequence
of instabilities or bifurcations cf. Schuster (1988) or Bergé et
al (1986), showing quasi-periodicity, period-doubling, or temporal
intermittency. In fluid flow these routes can be observed in the onset
range of heat convection in Rayleigh-Bénard systems (fluid heated
from below) or in Taylor-Couette systems (concentric cylinders, the
inner one rotating), see e.g. Koschmieder (1993). Laminar shear flows
between plane boundaries or through pipes stay linearly stable,
instead, but nevertheless become turbulent, though at larger Reynolds
numbers Re = O(1 000). The mechanism is not an eigenvalue instability
but a subtle interplay between nonnormal bunching of the
eigenstates and their nonlinear interaction, see Boberg and
Brosa (1988), Gebhardt and Grossmann (1993, 1994), Trefethen et al
(1993), Grossmann (1996, 1999). The most characteristic features are
the double threshold and a large phase space Hausdorff dimension at
onset. The threshold is fractal under a given type of perturbations and
in phase space a chaotic repeller (arising from unstable stationary
states) generates the complex, chaotic dynamics of turbulent flow,
Eckhardt et al (1998).
References
Bergé P, Pomeau Y and Vidal C 1986 Order within
Chaos-Towards a deterministic approach to turbulence (New York:
Wiley)
Boberg L and Brosa U 1988 Z. Naturforsch 43a 697
Eckhardt B, Marzinzik K and Schmiegel A 1998 in A Perspective
Look at Nonlinear Media
eds. J Parisi, S C Müller and
W Zimmermann Lecture Notes in Physics 503 (Berlin:
Springer) pp 327-338
Gebhardt T and Grossmann S 1993 Z. Phys. B90 475
Gebhardt T and Grossmann S 1994 Phys. Rev. E50 3705
Grossmann S in Nonlinear Physics of Complex Systems eds. J
Parisi, S C Müller and W Zimmermann Lecture Notes in
Physics 476 (Berlin: Springer) pp 10-22
Grossmann S 1999 Rev. Mod. Phys.
Koschmieder E L 1993 Bénard Cells and Taylor Vortices
(Cambridge: Cambridge University Press)
Schuster H G 1988 Deterministic Chaos-An Introduction
(Weinheim: VCH-Wiley)
Trefethen L N, Trefethen A E, Reddy S C and Driscol T A 1993
Science 261 578
Turbulent heat transport:
global performance-global scaling
Siegfried Grossmann
Fachbereich Physik der Philipps-Universität, Marburg, Germany
A temperature difference  between the bottom and the top
plates enclosing a gas or a liquid at rest imply molecular heat
transport. The heat current
between the bottom and the top
plates enclosing a gas or a liquid at rest imply molecular heat
transport. The heat current  is determined by, besides
is determined by, besides
 , the thermal conductivity
, the thermal conductivity 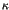 and the height
and the height 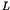 of the
fluid layer,
of the
fluid layer, 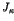 being
being
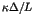 . If the
nondimensionalized temperature difference
. If the
nondimensionalized temperature difference
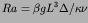 , the Rayleigh number of this Rayleigh-Bénard system,
becomes larger, the molecular heat transport is supported by
convective transport. Here
, the Rayleigh number of this Rayleigh-Bénard system,
becomes larger, the molecular heat transport is supported by
convective transport. Here  is the kinematic viscosity, g the
gravitational acceleration, and
is the kinematic viscosity, g the
gravitational acceleration, and 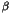 the thermal volume expansion
coefficient. At medium
the thermal volume expansion
coefficient. At medium 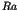 rolls of fluid flow with increasing velocity
rolls of fluid flow with increasing velocity
 are developed. For large
are developed. For large 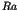 the flow in the bulk of the rolls
becomes turbulent. The heat current
the flow in the bulk of the rolls
becomes turbulent. The heat current 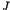 then can be carried by the
turbulent convection. This is very effective, so
then can be carried by the
turbulent convection. This is very effective, so 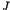 increases
with
increases
with 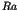 . The heat current, called the Nusselt number
. The heat current, called the Nusselt number 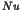 when
measured in multiples of the molecular current
when
measured in multiples of the molecular current 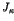 , i.e.,
, i.e.,
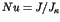 , depends algebraically on
, depends algebraically on 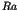 . It also scales
algebraically with the Prandtl number
. It also scales
algebraically with the Prandtl number 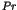 , which characterizes the
importance of the kinematic viscosity relative to the thermal
conductivity, i.e.,
, which characterizes the
importance of the kinematic viscosity relative to the thermal
conductivity, i.e.,
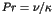 . The scaling exponents of the
heat current
. The scaling exponents of the
heat current 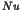 as well as of the roll velocity, measured by the roll
Reynolds number
as well as of the roll velocity, measured by the roll
Reynolds number
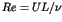 as functions of
as functions of 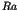 and
and 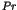 , the
control parameters, are derived and discussed in this lecture.
, the
control parameters, are derived and discussed in this lecture.
Since heat current  and roll velocity
and roll velocity  are global
responses of the fluid to the driving temperature difference only
global arguments turn out to determine the scaling behaviors with
are global
responses of the fluid to the driving temperature difference only
global arguments turn out to determine the scaling behaviors with 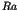 and with
and with 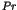 . It is suggested that the only relevant physical
quantities are the kinematic and the thermal dissipation rates. These
can be determined in the bulk as well as in the boundary layers.
Utilizing exact relations between the dissipation rates and the
currents
. It is suggested that the only relevant physical
quantities are the kinematic and the thermal dissipation rates. These
can be determined in the bulk as well as in the boundary layers.
Utilizing exact relations between the dissipation rates and the
currents 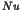 and
and 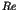 allows to derive the various scaling laws valid
in the different regions of the parameter space
allows to derive the various scaling laws valid
in the different regions of the parameter space 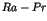 . We also give
the crossover corrections between regions, which jeopardize pure
scaling. Comparison with several previous and recent experiments
is very encouraging for this unifying theory of scaling in thermal
convection. The reference for this unifying theory is Grossmann and
Lohse (1998).
. We also give
the crossover corrections between regions, which jeopardize pure
scaling. Comparison with several previous and recent experiments
is very encouraging for this unifying theory of scaling in thermal
convection. The reference for this unifying theory is Grossmann and
Lohse (1998).
Introductory references to thermal convection are Koschmieder (1993),
Castaing et al. (1989); for information about experiments see Wu and
Libchaber (1991), Chavanne et al. (1997), Cioni et al. (1997);
theoretical overviews are given by Shraiman and Siggia (1990), Siggia
(1994); an extended list of references can be found in the cited
work by Grossmann and Lohse (1998).
References
Castaing B, Gunaratne G, Heslot F, Kadanoff L, Libchaber A, Thomae S,
Wu X Z, Zaleski S and Zanetti G 1989 J. Fluid Mech. 204 1
Chavanne X, Chilla F, Castaing B, Hebral B, Chaboud B and Chaussy J
1997 Phys. Rev. Lett. 79 3648
Cioni S, Ciliberto S and Sommeria J 1997 J. Fluid Mech. 335
111
Grossmann S and Lohse D 1998 Scaling in thermal convection: A
unifying theory submitted to J. Fluid Mech.
Koschmieder E L 1993 Bénard Cells and Taylor Vortices
(Cambridge University Press)
Shraiman B I and Siggia E D 1990 Phys. Rev. A42 3650
Siggia E D 1994 Annu. Rev. Fluid Mech. 26 137
Wu X Z and Libchaber A 1991 Phys.Rev. A43 2833
Energy dissipation in turbulent flow:
rigorous and less rigorous insights
Siegfried Grossmann
Fachbereich Physik der Philipps-Universität, Marburg, Germany
To maintain fluid flowing one needs stirring by some external force.
There is no
turbulence without ongoing energy input, which compensates the
permanent energy loss by viscous damping. Therefore the most relevant
quantity to characterize turbulence is the mean energy flow rate per
mass,
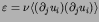 , and its dependence on the Reynolds number
, and its dependence on the Reynolds number
 .
From dimensional argument the energy flow
.
From dimensional argument the energy flow 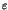 must be
must be
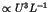 . The dimensionless prefactor, denoted as the
dissipation coefficient
. The dimensionless prefactor, denoted as the
dissipation coefficient
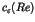 , is
, is 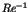 for laminar
flow. Its behavior for turbulent flow and in particular asymptotically
for large
for laminar
flow. Its behavior for turbulent flow and in particular asymptotically
for large
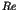 is of high interest.
is of high interest.
In this lecture, after introductory estimates of the dissipation
coefficient
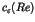 , a variational principle is derived,
leading to a rigorous upper bound of the dissipation rate's coefficient
(Nicodemus, Grossmann and Holthaus 1997). The variational principle is
formulated in terms of a static auxiliary field which is optimized to
carry the dissipation of the real turbulent flow field. It is one of
the few exact results on the nonlinear Navier-Stokes dynamics. This
principle is a generalization of Doering and Constantin's work (1992,
1994). Hopf (1941) was the first to study bounds on energy
dissipation with this idea. Another line of approach is the Busse (1970)
and Howard (1972) variational method; in that the flow field is
decomposed into its mean and the fluctuating deviations. Using our
results it could be shown (Kerswell 1997) that both methods lead to the
same bounds on energy dissipation. Asymptotically
, a variational principle is derived,
leading to a rigorous upper bound of the dissipation rate's coefficient
(Nicodemus, Grossmann and Holthaus 1997). The variational principle is
formulated in terms of a static auxiliary field which is optimized to
carry the dissipation of the real turbulent flow field. It is one of
the few exact results on the nonlinear Navier-Stokes dynamics. This
principle is a generalization of Doering and Constantin's work (1992,
1994). Hopf (1941) was the first to study bounds on energy
dissipation with this idea. Another line of approach is the Busse (1970)
and Howard (1972) variational method; in that the flow field is
decomposed into its mean and the fluctuating deviations. Using our
results it could be shown (Kerswell 1997) that both methods lead to the
same bounds on energy dissipation. Asymptotically
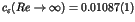 . From the volume mean one has to
distinguish the bulk dissipation, Sreenivasan (1984), Lohse (1994),
Grossmann(1995). Recently we identified for the first time a mechanism
that leads to a decrease of
. From the volume mean one has to
distinguish the bulk dissipation, Sreenivasan (1984), Lohse (1994),
Grossmann(1995). Recently we identified for the first time a mechanism
that leads to a decrease of
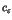 with
with
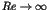 , Nicodemus, Grossmann and Holthaus (1999). The
lecture finishes with a comparison of the kinetic dissipation with the
thermal dissipation in heat convection (Nicodemus, Grossmann and
Holthaus, unpublished). More details about the mathematical and the
numerical methods for d-dimensional bounds, also for
the
, Nicodemus, Grossmann and Holthaus (1999). The
lecture finishes with a comparison of the kinetic dissipation with the
thermal dissipation in heat convection (Nicodemus, Grossmann and
Holthaus, unpublished). More details about the mathematical and the
numerical methods for d-dimensional bounds, also for
the 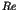 -asymptotics, can be found in Nicodemus, Grossmann and
Holthaus (1997, 1998, 1999).
-asymptotics, can be found in Nicodemus, Grossmann and
Holthaus (1997, 1998, 1999).
References
Busse F H 1970 J. Fluid Mech. 41 219
Busse F H 1978 Adv. Appl. Mech. 18 77
Doering C R and Constantin P 1992 Phys. Rev. Lett. 69 1648
Doering C R and Constantin P 1994 Phys. Rev. E49 4087
Grossmann S 1995 Phys.Rev. E51 6275
Hopf E 1941 Math Annalen 117 764
Howard L N 1972 Annu. Rev. Fluid Mech. 4 473
Kerswell R R 1997 Physica D100 355
Lohse D 1994 Phys. Rev. Lett. 73 3223
Nicodemus R, Grossmann S and Holthaus M 1997 Physica D101
178
Nicodemus R, Grossmann S and Holthaus M 1997 Phys. Rev. Lett.
79 4170
Nicodemus R, Grossmann S and Holthaus M 1997 Phys. Rev. E56
6774
Nicodemus R, Grossmann S and Holthaus M 1998 J. Fluid Mech.
363 281
Nicodemus R, Grossmann S and Holthaus M 1998 J. Fluid Mech.
363 301
Nicodemus R, Grossmann S and Holthaus M 1999 "Towards lowering
dissipation bounds" Eur. Phys. J B in press
Sreenivasan K R 1984 Phys. Fluids 27 1048
Brain dynamics - Part I
Hermann Haken
Center of Synergetics, Stuttgart, Germany
The human brain is the most mysterious organ we know of. In it perception,
speech control, thinking, feelings, emotions, and many other things exist.
Seen from the point of view of a physicist, it is the most complex system in
the world. It consists of about a hundred billion of neurons that are
interconnected in a highly complicated fashion.
In my lectures I will address two main topics:
1. The explicit example of a neural net (the lighthouse model)
2. How do macroscopic features, such as perception or motor-control, arise from
microscopic elements.
The vehicle I shall use to study the second question is synergetics. In my
first lecture I wish to remind the audience of some physical methods to study
brain functions, such as EEG, MEG, PET and MRI. In order to understand the
macroscopic activity patterns of the brain, basic concepts of synergetics
will be used and a reminder will be given of basic concepts, such as control
parameters, instability, order parameters, slaving principle, critical
fluctuations, and symmetry breaking in open systems far from thermal
equilibrium. These concepts are exemplified by phenomena of visual perception,
such as bistability, hysteresis, and oscillations. The synergetic computer
will serve as a model for pattern recognition and links with Gestalt theory
will be established.
References
H. Haken, Principles of Brain Functioning, Springer, Berlin (1996)
J.A.S. Kelso, Dynamic Patterns, MIT Press (1995)
Brain dynamics - Part II: The lighthouse model of a neural net
Hermann Haken
Center of Synergetics, Stuttgart, Germany
I present some salient features of neurons and their connections, and I discuss
the role of soma, axon, dendrites and synapses. I briefly sketch previous
models, such as that of McCulloch and Pitts, Wilson and Cowan, Jirsa and Haken,
which neglect phase relations, and models that deal with phase couplings
(Kuramoto, Tass), with sinusoidal couplings, and integrate and fire models
(Strogatz et al., Geisel et al.).
I then present the basic concepts of the lighthouse model of a neural net as
developed by the present author, where attention is focused on phase-locking
by means of pulse trains. Basic variables are dendritic currents that are
generated by axonal pulses and phases describing the timing of the axonal
pulses. The latter are generated by dendritic currents, processed by the soma
of a neuron. While below a threshold, the neuron is, as usually assumed,
quiescent, according to my model above that threshold its firing rate increases
linearly with the inputs.
References
McCulloch and W. Pitts, Bulletin of Math. Biophysics 5, 115-133
(1943)
H.R. Wilson and J.D. Cowan, Biophysical Journal 12, 1-24 (1972)
V.K. Jirsa and H.Haken, Phys. Rev. Lett. (1996); Physica D (1997)
Y. Kuramoto and I. Nishikawa, J. Stat. Phys. 49, 569 (1987); Y.
Kuramoto, Physica D 50, 15 (1991)
P. Tass and H. Haken, Z. Phys. B 100, 303-320 (1996); Biol.
Cybern. 74, 31-39 (1996)
C. Uhl, Analysis of Neurophysiological Brain Functioning, Springer,
Berlin (1999)
R.E. Mirollo and S.H. Strogatz, SIAM (Soc. Ind. Appl. Math.) J. Appl.
Math. 50, 1645 (1990)
U. Ernst, K. Pawelzik and T. Geisel, Physical Review E 57, no. 2
(1998)
Brain dynamics - Part III: Steady states, mutual interaction and
associative memory of the lighthouse model
Hermann Haken
Center of Synergetics, Stuttgart, Germany
Though the model is highly nonlinear, because of the occurrence of pulses, it
can be treated exactly. Especially the case of small damping of the dendritic
currents leads to very elegant results. The elimination of the variables
describing the dendritic currents leads to phase-equations. By means of the
example of two neurons, I demonstrate how the steady state can be calculated.
This leads to a mutual activation of neurons so that neurons become active
even if they have been below threshold because of a too weak sensory input.
I then treat the case of an arbitrary number of neurons that are arbitrarily
coupled with each other and are subject to arbitrary sensory inputs. The
activation of patterns shows up in specific pulse rates, and the action of
the whole net can be interpreted as that of a associative memory. I distinguish
between weak and strong associative memory and explain the application of this
concept to Kaniza figures.
Brain dynamics - Part IV: Phase-locking of two and many neurons, impact
of noise and delayed interactions
Hermann Haken
Center of Synergetics, Stuttgart, Germany
In this part it is assumed that all sensory inputs are equal, but the coupling
between the neurons may still be arbitrary. I start from a phase-locked state
and derive equations for deviations from that state. The deviations may have
different causes, namely resetting of the individual phases externally, or
internal noise. In this way I demonstrate the stability of the phase-locked
state against these perturbations. On the other hand, if a pulse is lacking due
to failure of a vesicle, or an additional pulse is emitted due to spontaneous
opening of a vesicle, a phase lag is caused. The results can be extended to an
arbitrary net and delayed interactions, provided the delay-time is the same
for all neurons.
Brain dynamics - Part V: Phase averaged equations
Hermann Haken
Center of Synergetics, Stuttgart, Germany
I show how the lighthouse model and phase averaged equations, such as the
Nunez and Jirsa-Haken equations, are related to each other. I will discuss
a number of open problems.
References
P.L. Nunez, Oxford University Press, Oxford (1995)
V.K. Jirsa and H.Haken, Phys. Rev. Lett. (1996); Physica D (1997)
Random matrix theories and the problem of
Anderson localization
Hiroshi Hasegawa
Research Center of Quantum Communications, Tamagawa University, Macida,
and
Atomic Energy Research Institute, Nihon University, Kanda-Surugadai,
Tokyo
The problem ``Anderson localization" is one of major subjects in
Condensed Matter Physics, and in recent years it has been explored
intensively from a viewpoint of quantum level statistics[1].
Historically, this emphasis has occurred from a technical development in
the decade of 80's about Gaussian mean over matrix ensembles by the
method of supersymmetry that implemented studies of correlation
functions[2]. An interest in the subject is the intermediate nature of
the statistics between the standard Wigner-Dyson (in the metallic phase)
and the Poisson (in the localized phase): it would be a
level-statistical evidence of the phase transition between these two
phases. Among numerous works on this subject in the past decade, the
results provided by Al'tshuler and coworkers should not be
overlooked[4-6][8-11]. In the present lecture, therefore, we focus our
attention on the most interesting result due to them, namely the
compressibility of level gas at the mobility edge.
References
1. B.L.Al'tshuler,Universalities: from Anderson
localization to quantum chaos in Mesoscopic Quantum Physics
LesHouches Session LXI ed. E. Akkermans, G.
Montambaux, J.-L.
Pichard, and J.
Zinn-Justin(ELSEVIER, Amsterdam1995).
2. T. Guhr, A. Müller-Groeling,and H. A. Weidenmüller,
Random Matrix Theories in Quantum Physics: Common Concepts, Phys.
Rep.299(1998), 189.
3. M. Toda, R. Kubo,and N. Sait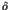 Statistical
Physics I
2nd ed. Springer-Verlag Berlin(1992).
Statistical
Physics I
2nd ed. Springer-Verlag Berlin(1992).
4. B. L. Al'tshuler and B. I. Shklovskii, Sov. Phys. JETP
64(1986), 127.
5. B. L. Al'tshuler, I. Kh. Zharekeshev, S. A. Kotochigova and
B. I. Shklovskii, Sov. Phys. JETP67(1988), 625.
6. V. E. Kravtsov, I. V. Lerner,B. L. Al'tshuler and A. G.
Aronov, Phys. Rev. Lett.72(1994), 888; A. G. Aronov, V. E.
Kravtsov and I.V. Lerner, Sov. Phys. JETP Lett. 59(1994), 39.
7. M. L. Mehta and F. J. Dyson, J. Math. Phys.4(1963), 713.
8. A. G. Aronov, V. E. Kravtsov and I. V. Lerner, Phys. Rev.
Lett.74(1995), 1174; V. E. Kravtsov and I. V. Lerner,Phys. Rev.
Lett. 74(1995), 2563.
9. A. G. Aronov and A. D. Mirlin, Phys. Rev. B51(1995), R6131.
10. J. T. Chalker, I. V. Lerner and R. Smith, Phys. Rev.
Lett.77(1996), 554; J. Math. Phys.37(1996), 5061.
11. J. T. Chalker, V. E. Kravtsov and I. V. Lerner, JETP Lett.64
(1996), 386.
Random Matrix Theories and the Problem of
Anderson Localization II
Hiroshi Hasegawa
Research Center of Quantum Communications, Tamagawa University, Macida,
and
Atomic Energy Research Institute, Nihon University, Kanda-Surugadai,
Tokyo
There exists a framework of computing two-point correlation
function between
a pair of levels of a random eigenvalue sequence that is supposed to
arise from a perturbed hermitian
 , where
, where  belongs to a
set of fully uncorrelated Hermitians (a Poisson ensemble) and
belongs to a
set of fully uncorrelated Hermitians (a Poisson ensemble) and 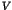 to a
set of Hermitians in the Wigner-Dyson class (one of the three standard
RMT ensembles)[12-15]: it has been regarded as adapted for level
statistics with Anderson transition[15]. This correlation function
to a
set of Hermitians in the Wigner-Dyson class (one of the three standard
RMT ensembles)[12-15]: it has been regarded as adapted for level
statistics with Anderson transition[15]. This correlation function
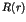 has two remarkable characteristics. (1) its long-range
behavior (
has two remarkable characteristics. (1) its long-range
behavior ( ) reflects an attractiveness between the pair of
levels (
) reflects an attractiveness between the pair of
levels ( [12,13]), and (2)
[12,13]), and (2)
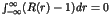 [14].
We argue that (1) may be regarded as the characteristic of
level statistics in a metallic phase[16] that could undergo
Anderson transition, whereas (2) contradicts the existence of an
intermediate compressibility[10,11]. Here, we present a new framework
adapted for Anderson transition based on equilibrium statistical
mechanics of level gas[18-22] (a Hamiltonian level dynamics for
[14].
We argue that (1) may be regarded as the characteristic of
level statistics in a metallic phase[16] that could undergo
Anderson transition, whereas (2) contradicts the existence of an
intermediate compressibility[10,11]. Here, we present a new framework
adapted for Anderson transition based on equilibrium statistical
mechanics of level gas[18-22] (a Hamiltonian level dynamics for
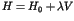 ) satisfying (1) and, furthermore, capable for the
intermediate compressibility.
References
) satisfying (1) and, furthermore, capable for the
intermediate compressibility.
References
12. F. Leyvraz and T. H. Seligman, J. Phys. A: Math. Gen.
23(1990),1555.
13. T. Guhr, Phys.Rev.Lett.76(1996),2258;
Ann.Phys.(N.Y.)250(1996),145.
14. H. Kunz and B. Shapiro, Phys. Rev. E58(1998),400.
15. K. M. Frahm, T. Guhr and A. Müller-Groeling,
Ann.Phys.(N.Y.)
270 (1998),292.
16. R.A.Jalabert, J.-L.Pichard and C.W.J. Beenakker, Europhys.
Lett. 24(1993),1.
17. D. Weinmann and J.-L.Pichard, Phys.Rev.Lett.
77(1996),1556.
18. M. Gaudin, Nucl. Phys.85(1966),545; T. Yukawa, Phys.
Rev. Lett.54(1985),1883; Phys. Lett.A116(1986),227.
19. H. Hasegawa and J.-Z. Ma, J. Math. Phys.39(1998),2564.
20. H. Hasegawa Information Theory and Statistical Mechanics
of Random Matrices, RIMS publication 1066(1998),205; Open
Sys. and Information Dyn.(1999),to be published.
21. J.-L. Pichard and B. Shapiro, J.Phys.I (France)
4(1994),623.
22. P.J. Forrester, Phys. Lett.A173(1993),355.
23. D. Ruelle,Statistical Mechanics(W.A. Benjamin,Inc. New
York, 1969).
From small to large scale activity of
spatiotemporal neural patterns
Viktor K. Jirsa
Center for Complex Systems and Brain Sciences,
Florida Atlantic University, Boca Raton, USA
The neuron is thought to be the central microscopic
information-processing unit
in the brain. We review its morphology (see Braitenberg
and Schüz (1991))
and dynamics and discuss mathematical models of neuronal
temporal activity
(Hodgkin-Huxley, integrate-and-fire and spike-response
model; see e.g. Kistler
et al (1997) ). Interconnectivity among neurons
requires to
traverse to a description of neural networks. In many
areas of the brain
neurons are organized in populations of units with
similar properties which
allows to describe the mean activity of a neuronal
population rather than the
temporal behavior of individual neurons. Spatiotemporal
neural activity in
terms of neural ensembles
has been described by Wilson and Cowan (1972,1973) and
Nunez (1974).
Later approaches by Jirsa and Haken (1996) and others
unified and generalized
these models to a neural field theory on large
spatiotemporal scales
accessible to electroencephalography (EEG) and
magnetoencephalography (MEG).
The introduction of the notion of ``Functional units" by
Jirsa and Haken (1996)
provides a means to correlate behavioral patterns to EEG
and MEG patterns (for
the specific realization of Bimanual Coordination see
Jirsa et al (1998), for
reviews of large scale brain and behavioral dynamics see
Kelso (1995), Nunez
(1995), Haken (1996)).
References
Braitenberg V and Schüz A (1991) Anatomy of the
cortex.
Statistics and geometry (Springer, Berlin)
Haken H (1996) Principles of Brain Functioning
(Springer, Berlin)
Jirsa V K and Haken H (1996) Phys. Rev. Let.
77 960
Jirsa V K, Fuchs A and Kelso J A S (1998) Neur.
Comp. 10 2019
Kelso J A S (1995) Dynamic Patterns. The
Self-Organization of Brain and
Behavior (The MIT Press, Cambridge, Massachusetts)
Kistler W M, Gerstner W and van Hemmen J L (1997)
Neur. Comp. 9
1015
Nunez P L (1974) Math. Biosci. 21 279
Nunez P L (1995) Neocortical Dynamics and Human EEG
Rhythms (Oxford
University Press, Oxford)
Wilson H R and Cowan J D (1972) Biophys. J.
12 1
Wilson H R and Cowan J D (1973) Kybernetik
13 55
Spatiotemporal pattern formation in systems with
heterogeneous connection
topology
Viktor K. Jirsa
Center for Complex Systems and Brain Sciences,
Florida Atlantic University, Boca Raton, USA
We briefly review spatiotemporal pattern formation via
self-organization in
open non-equilibrium systems of different nature, e.g.
in physical systems as
in hydrodynamics or the laser, in chemical systems as in
the Belousov
Zhabotinsky reaction (see Haken 1975, Cross and
Hohenberg 1993 for reviews).
In these systems the underlying connection topology is
typically homogeneous,
i.e. translationally invariant, which provides the basis
for modelling their
spatiotemporal dynamics by nonlinear partial
differential equations as in the
Ginzburg-Landau theory (see Haken (1983)). This approach
has been applied
successfully to a class of biological systems for which
the connection
topology may be assumed to be regular such as coat
markings of mammals or fish
(see Murray (1993) for review). However, many biological
systems such as the
human cortex show homogeneous connectivity with
additional strongly
heterogeneous projections from one area to another (see
Braitenberg and
Schüz 1991, Felleman and Van Essen 1991), but still
perform coherent
spatiotemporal pattern formation (see Kelso (1995)).
Such heterogeneous
connectivity may undergo temporal changes via mechanisms
of asymmetric
Hebbian learning or synaptic plasticity (see Markram et
al (1997)). Here we
show mathematically and numerically how the global
spatiotemporal dynamics of a
heterogeneously connected system can be controlled via
local changes in the
connection topology and thus be guided through a series
of non-equilibrium
phase transitions.
We provide a mathematical description of the system in
terms of a nonlinear
integral equation which is retarded by delays via
propagation of signals along
connecting pathways (see Jirsa and Haken (1996)). Our
formulation allows to
use the connectivity as a topological control parameter
which could not be
achieved by means of partial differential equations in a
straight forward way.
References
Braitenberg V and Schüz A (1991) Anatomy of the
cortex.
Statistics and geometry (Springer, Berlin)
Cross M C and Hohenberg P C (1993) Rev. Mod. Phys.
65 851
Felleman D J and Van Essen D C (1991) Cerebral
Cortex 1 1
Haken H (1975) Rev. Mod. Phys. 47 67
Haken H (1983) Synergetics. An Introduction
(Springer, Berlin)
Jirsa V K and Haken H (1996) Phys. Rev. Let.
77 960
Kelso J A S (1995) Dynamic Patterns. The
Self-Organization of Brain and
Behavior (The MIT Press, Cambridge, Massachusetts)
Markram H, Lübke J, Frotscher M and Sakmann B (1997)
Science 275
213
Murray J D (1993) Mathematical Biology (2nd ed.,
Springer, Berlin
Heidelberg New York)
Control of chaos in the heart: New approaches, problems
Alain Pumir and Valentin Krinsky
Institut Non Linéaire de Nice
U.M.R. 6618, C.N.R.S. Université de Nice Sophia -
Antipolis, Valbonne, France.
We review the main ideas and results in the mathematical theory of
chaotic wave propagation in cardiac muscle. Mechanisms of chaos
and approaches to control the chaos are understood for
ordinary differential equations (d.e.), but for partial d.e,
only isolated results are published.
In cardiac muscle, the chaotic regime known as fibrillation is
the main reason of mortality in industrial world. A very strong
electrical discharge (defibrillation) eliminates the chaos.
Mechanisms of defibrillation are poorly understood. Important is
to study alternative approaches to eliminate the chaos.
For cardiac muscle (and excitable media in general), the initial
stage in transition to chaos is formation of rotating vortices.
Elimination of vortices at this stage effectively prevents chaos
development. We study two different kind of vortices, free
vortices, and vortices pinned to a defect. We found that a weak
shock, with an amplitude an
order of magnitude less than the defibrillating shock, may
unpin the vortices rotating around the defects (obstacles). The
unpinning results from a depolarization of the tissue near the
obstacle,
induced by an external electric field within a distance of order
electrical space constant in cardiac muscle  (Weidmann,
1970).
Unpinning was observed both in the Fitz Hugh model of
excitable tissue,
and in a specific Beeler-Reuter model of cardiac tissue. This
theoretical
observation suggests that anatomical reentries can be transformed
into functional reentries, an effect that can be tested
in experiments with cardiac muscle.
(Weidmann,
1970).
Unpinning was observed both in the Fitz Hugh model of
excitable tissue,
and in a specific Beeler-Reuter model of cardiac tissue. This
theoretical
observation suggests that anatomical reentries can be transformed
into functional reentries, an effect that can be tested
in experiments with cardiac muscle.
References
J. Keener and J. Sneyd.
Mathematical Physiology,
Springer- Verlag, New York, 1998.
Pumir, A., Plaza, F., Krinsky , V.
Control of rotating waves in cardiac muscle:
analysis of the effect of the electric field.
Proc Roy Soc B, 257, 129-134, 1994. 0D
A. Pumir, V. Krinsky.
How does an electric field defibrillate cardiac muscle?
Physica D, 91, 205 - 219, 1996.
V. Krinsky and A.Pumir
Models of defibrillation of cardiac tissue
Chaos, 8, n.1, p.188-203, 1998
V. Krinsky
Qualitative theory of reentry
In Cardiac Electrophysiology, 46rom Cell to Bedside, D.P.
Zipes and J.Jalife, editors, chapter 38, Saunders,
Philadelphia, 1998.
Phase dynamics -- Its conceptual universality
and different
specific forms --
Yoshiki Kuramoto
Graduate School of Sciences, Kyoto University, Japan
Our understanding of the dynamics of many nonlinear
dissipative systems relies crucially upon the possibility that under
various conditions
complicated nonlinear evolution equations could be reduced to far simpler
forms. This lecture is devoted to clarifying the theoretical grounds for
such dynamical reduction with particular emphasis on the phase dynamics.
We first argue that, explicit or implicit,
virtually all theories of reduction involve commonly one universal feature,
namely, a perturbative construction of an attracting invariant manifold
together with a definition of an appropriate coordinate system on
this manifold in such a way that the evolution law there may look as simple as
possible. This assertion is then demonstrated for the two of the most
fundamental
reduction methods, i.e., the center-manifold reduction and the phase
reduction. Here, the trivial invariant manifold to start with
is given by the critical eigenspace in the first case, and the neutral
space spanned by the Goldstone mode in the second case. We also discuss
how the reduction idea developed for ODEs, where such perturbative methods
presuppose low-dimensionality
of the invariant manifold, can immediately be carried over to PDEs with
large spatial extension for which the dimension of the invariant manifold
should practically be infinite. From such a viewpoint, the Chapman-Enskog
reduction, a monumental reduction theory of nonequilibrium statistical
mechanics, turns out almost identical in structure with the phase
dynamics.
As a separate topic of reduction, a different form of phase reduction
particularly adapted to coupled oscillators systems will be presented,
and we demonstrate its usefulness through the derivation of phase
equations in various situations of practical interest.
References
Mori H and Kuramoto Y 1998 Dissipative Structures and Chaos
(Berlin Heidelberg: Springer-Verlag) Ch. 5
Chapman S and Cowling T. G. 1970 The Mathematical Theory of
Nonuniform Gases 3rd. Ed. (Cambridge: Cambridge Univ. Press)
Kuramoto Y 1984 Chemical Oscillations, Waves, and Turbulence
(Berlin: Springer-Verlag)
Collective dynamics of coupled oscillators
Yoshiki Kuramoto
Graduate School of Sciences, Kyoto University, Japan
Numerous examples of interacting rhythmic processes are found in various
fields of science including physics, chemistry and biology, and their
proper mathematical description can be provided by dynamical systems of
coupled limit-cycle oscillators. In this lecture, we will discuss
the dynamics of large populations of oscillators with mean-field coupling,
and present an overview of various theoretical approaches developed up to
this day since the pioneering work of Winfree (1967). We describe
in some detail a prototypal phase oscillator model with distributed
native frequencies (Kuramoto 1975) which admits
an exact solution for the phase transition due to mutual synchronization.
This model and its generalizations have been analyzed more deeply, and also
found some important applications. Some of the important works among them
will be surveyed. They include Strogatz et al's theory on the stability of
the collective states, Crawford's center-manifold reduction of the model
with external noise, Daido's generalization of the coupling function
in terms of the order function, and Wiesenfeld et al's proof of
the equivalence of the original model with circuit equations for
certain series arrays of Josephson
junctions.
We also describe the possibility of nontrivial forms of collective dynamics,
e.g., clustering, bursting and collective chaos, some of which may have
implication in biological information processing.
Aside from collective dynamics, there are many applications of the
phase reduction method itself, e.g, to the construction
of the phase-coupling function for various realistic models,
which will also be touched upon.
References
Winfree A T 1967 J. Theor. Biol. 16 15
Kuramoto Y 1975 in International Symposium on Mathematical Problems
in Theoretical Physics, Lecture Notes in Physics Vol. 39, ed. by Araki H
(Berlin: Springer-Verlag) 420
Strogatz S H et al. 1992 Phys. Rev. Lett. 68 2730
Crawford J D 1994 J. Stat. Phys. 74 1047
Daido H 1996 Physica D 91 24
Wiesenfeld et al 1998 Phys. Rev. Lett. 57 1563
Golomb D et al. 1992 Phys. Rev. A 45 3516
Hansel D et al. 1993 Phys. Rev. E 48 3470
Hakim V and Rappel W J 1992 Phys. Rev. A 46 R7347
Nakagawa N and Kuramoto Y 1993 Prog. Theor. Phys. 89 313
Han S K et al. 1995 Phys. Rev. Lett. 75 3190
Turbulence with multiscaling in large assemblies
of oscillators
Yoshiki Kuramoto
Graduate School of Sciences, Kyoto University, Japan
We discuss a universal class of turbulent states discovered recently in
a wide variety of nonequilibrium systems including nonlocally coupled
chaotic and non-chaotic oscillators, arrays of uncoupled oscillators
with long-wave random forcing, and certain types of 3-component
reaction-diffusion systems. The turbulence here is characterized by
multiscaling properties of the structure functions, which is reminiscent
of fully developed Navier-Stokes turbulence. Specifically, various moments
of the amplitude increments between two points exhibit a power-law
dependence on the mutual distance. As a consequence, the amplitude profile
is fractal with multi-affine properties. Remarkably, the fractal dimension
changes continuously with the system parameter, and there is a critical
condition beyond which the amplitude profile completely loses the
spatial continuity, disintegrating into infinitesimal pieces.
We develop a theory based on a multiplicative stochastic process obeyed by
the amplitude increments, and discuss its approximate stationary solutions
from which all multiscaling properties as well as the
continuity-discontinuity transition can be explained.
It is also argued that the field defined by a coarse-grained spatial derivative
of the amplitude is characterized by multifractals, which is again
reminiscent of the multifractal nature of the energy dissipation field
in fully developed turbulence. Such properties are, however, by no means
direct consequences
of the multiscaling of the original field, and some attempts will be made
toward their understanding.
References
Kuramoto Y 1995 Prog. Theor. Phys. 94 321
Kuramoto Y and Nakao H 1996 Phys. Rev. Lett. 76 4352
Kuramoto Y and Nakao H 1997 Phys. Rev. Lett. 78 4039
Kuramoto Y, Battogtokh D and Nakao H 1998 Phys. Rev. Lett. 81 3543
Nakao H 1998 Phys. Rev. E 58 1591
Nakao H and Kuramoto Y 1999 Eur. Phys. J. B (to appear)
Bohr T et al. 1998 Dynamical Systems Approach to Turbulence
(Cambridge)
Frisch U 1995 Turbulence -- The Legacy of A. N. Kolmogorov
(Cambridge)
Chaos and order in high energy physics and Yang-Mills theories
Viatcheslav I. Kuvshinov
Institute of Physics, Minsk, Belarus
Chaos and fractal signatures in high-energy physics processes are
discussed. In particular intermittency phenomenon, fractal jets and
clusters are analysed.
All four fundamental physical interactions have Yang-Mills gauge
nature and all of them have chaotic classical solutions in specific cases.
The talk reviews some situations when YM field theories have chaos-order
transition (at corresponding controlling parameters): non-Abelian nature,
monopoles, sphalerons, other topological solutions, Higgs fields, etc are
discussed as sources of chaos and order. For example, it is known that
Higgs fields--a very important element of gauge theories giving masses
to the particles--in its vacuum state can suppress chaos. Here it is shown
that non-vacuum states of Higgs fields can both suppress and induce
chaos.
Numerical and analytical methods of study of chaos properties of YM
theories are reviewed.
The problem of the description of quantum chaos in second quantized field HEP
theories is mentioned and its physical role questioned.
Some unsolved problems of modern HEP models such as
confinement of color quarks and gluons and their possible connections with
presence of chaos as immanent property of YM-equations are discussed.
References
Babichev L.F., Klenitsky D.V., Kuvshinov V.I. (1995)Phys.Lett.
B345
269
De Wolf E.A., Dremin I.M., Kittel W. (1996)Phys.Rep. 270 1
Hwa R. Correlations and Fluctuations W.Sci. (1996)pp.303-313
Kawabe T., Ohta S. (1991)Phys.Rev.D44 1274
Kawabe T. (1993)J.Phys.A.:Math.Gen.26 L1131
Kawabe T., Ohta S. (1994)Phys.Lett.B334 127
Kuvshinov V.I.(1995) Chaos and Complexity Editions Frontieres pp.197-200
Kuvshinov V.I. et al (1998)NPCS1 114
Kuvshinov V.I., Kuz'min (1999) Nonlinear Phenomena in Complex Systems Minsk
Mandelbaum G. (1995) Chaos and Complexity Editions Frontieres pp.193-196
Matinyan S.G., Prokhorenko E.B., Savidy G.K.(1986)JETF Lett 44 138
Rugh S.E.(1994) Aspects of Chaos of Fundamental Interactions. Part 1 Non-
Abelian Gauge Fields Licentiate Thesis. The Niels Bohr Institute
Salasnich L. (1995) Mod.Rev.Lett. A10 3119
Salasnich L. (1997) Symmetry in Physics, JINR Dubna
Savidy G.K.(1984) Nucl.Phys B246 302
Veneziano G. (1997) Int. Conf. on HEP, Springer pp.324-336
Pattern formation in bacterial colonies
Mitsugu Matsushita
Department of Physics, Chuo University,
Tokyo, Japan
We have studied the growth mechanism and morphological change in colony
formation of bacteria from the viewpoint of physics of pattern formation.
Even very small number of bacterial cells, once they are inoculated on the
surface of an appropriate medium such as semi-solid and nutrient-rich agar
plate and incubated for a while, repeat the growth and cell division
many times.
Eventually the cell number of the progeny bacteria becomes huge, and they
swarm on the medium to form a visible colony.
The colony differs in size, form, and color according to bacterial species.
It also changes its form sensitively with the variation of environmental
conditions.
This implies that although usual bacteria such as Escherichia coli are
regarded as single cell organisms, they never make their colony independently
and randomly but somehow collaborate multicellularly.
We have thus tried to extract some simple and universal behaviors in growth
from such complex bacterial systems.
Here we varied only two parameters to investigate the colony growth;
concentrations of nutrient  and agar
and agar 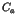 in a thin agar
plate as the incubation medium.
Other parameters specifying experimental conditions such as temperature were
kept constant.
We mainly used a typical bacterial species Bacillus subtilis.
Otherwise the experimental procedures are standard.
It was found that colonies show characteristic patterns in the specific
regions of values of
in a thin agar
plate as the incubation medium.
Other parameters specifying experimental conditions such as temperature were
kept constant.
We mainly used a typical bacterial species Bacillus subtilis.
Otherwise the experimental procedures are standard.
It was found that colonies show characteristic patterns in the specific
regions of values of 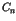 and
and  in the morphological diagram and
the patterns change drastically from one region to another.
They were classified into five types; fractal DLA-like, compact Eden-like,
concentric ring-like, simple disk-like and densely branched DBM-like.
We have experimentally elaborated characteristic properties for each of these
colony patterns.
We have also tried to construct a phenomenological but unified model which
produces characteristic colony patterns observed in our experiments.
It is a reaction-diffusion type model for the population density of bacterial
cells and the concentration of nutrient.
The essential assumption is that there exist two types of bacterial cells;
active cells that move actively, grow and perform cell division, and
inactive ones that do nothing at all.
We have varied values of the initial nutrient concentration and the ratio of
diffusion rate of bacterial cells to that of nutrients.
They correspond to the specified nutrient concentration in agar plates and
the substrate softness in our experiments, respectively.
Our model is found to be able to globally reproduce all the colony patterns
described above, and is phenomenologically quite satisfactory.
in the morphological diagram and
the patterns change drastically from one region to another.
They were classified into five types; fractal DLA-like, compact Eden-like,
concentric ring-like, simple disk-like and densely branched DBM-like.
We have experimentally elaborated characteristic properties for each of these
colony patterns.
We have also tried to construct a phenomenological but unified model which
produces characteristic colony patterns observed in our experiments.
It is a reaction-diffusion type model for the population density of bacterial
cells and the concentration of nutrient.
The essential assumption is that there exist two types of bacterial cells;
active cells that move actively, grow and perform cell division, and
inactive ones that do nothing at all.
We have varied values of the initial nutrient concentration and the ratio of
diffusion rate of bacterial cells to that of nutrients.
They correspond to the specified nutrient concentration in agar plates and
the substrate softness in our experiments, respectively.
Our model is found to be able to globally reproduce all the colony patterns
described above, and is phenomenologically quite satisfactory.
References
Matsushita M 1997 in Bacteria as Multicellular Organisms
eds. J A Shapiro and M Dworkin (New York: Oxford UP) pp366-393
Matsushita M, Wakita J and Matsuyama T 1995 in Spatio-Temporal Patterns in
Nonequilibrium Complex Systems, Proceedings Volume XXI of Santa Fe Institute
Studies in the Sciences of Complexity, eds. P E Cladis and P Palffy-Muhoray
(Reading: Addison-Wesley) pp609-618
Matsuyama T and Matsushita M 1993 CRC Critical Reviews in Microbiology
19 117
Wakita J, Ràfols I, Itoh H, Matsuyama T and Matsushita M 1998 J. Phys.
Soc. Jpn. 67 3630
Wakita J, Itoh H, Matsuyama T and Matsushita M 1997 J. Phys. Soc. Jpn.
66 67
Matsushita M, Wakita J, Ràfols I, Itoh H, Matsuyama T, Sakaguchi H and
Mimura M 1998 Physica A 249 517
Spatiotemporal patterns produced by bacteria
Mitsugu Matsushita
Department of Physics, Chuo University,
Tokyo, Japan
The growth of bacterial colonies is a ``Treasure Island'' of pattern
formation.
Apparently, the pattern-forming members (bacterial cells) are strongly
interacting, self-reproducible and self-driven ``particles'', very different
from conventional physical systems.
Some colony patterns grown on the surface of agar plates can be understood in
terms of well-defined models of pattern formation such as DLA, but not in all
cases.
Here we used a bacterial species Proteus mirabilis.
This species has been well-known for more than a century to form
macroscopically almost perfect concentric-ring like colonies with
approximately equal spacings on the surface of semi-solid substrate such as
an agar plate.
However, when this Proteus mirabilis was inoculated and incubated on
the surface of a very soft agar medium with rich nutrient, we observed that
entirely different, spatiotemporal patterns emerge inside a colony after
the colony spreads over the whole surface of the agar medium.
These spatiotemporal patterns include target and rotating spiral patterns.
In this sense the emerging patterns are very similar to those seen in
dissipative systems such as chemical oscillators and liquid-crystalline
electrohydrodynamic convective systems.
They also seem to exhibit characteristic features of spatiotemporal chaos.
Microscopic observations revealed that the two-dimensional collective motion
of bacterial cells seems to be responsible for the formation of the observed
spatiotemporal patterns.
Emphasis is also put on the construction of morphological diagram for
obtaining some clue to elucidate the growth mechanism and sometimes finding
new morphologies as well.
Examples are shown for bacterial colony formation and crystal growth in
gelatin gels.
References
Matsushita M 1997 in Bacteria as Multicellular Organisms
eds. J A Shapiro and M Dworkin (New York: Oxford UP) pp366-393
Rauprich O, Matsushita M, Weijer C J, Siegert F, Esipov S E and Shapiro J A
1996 J. Bacteriology 178 6525
Shimada Y, Nakahara A, Matsushita M and Matsuyama T 1995
J. Phys. Soc. Jpn. 64 1896
Moriyama O and Matsushita M 1995
J. Phys. Soc. Jpn. 64 1081
Nakahara A, Shimada Y, Wakita J, Matsushita M and Matsuyama T 1996
J. Phys. Soc. Jpn. 65 2700
Suda J, Nakayama T, Nakahara A and Matsushita M 1996
J. Phys. Soc. Jpn. 65 771
Suda J, Nakayama T and Matsushita M 1996
J. Phys. Soc. Jpn. 67 2981
Formation of colony patterns by a bacterial cell population
Mitsugu Matsushita
Department of Physics, Chuo University,
Tokyo, Japan
Bacterial species Bacillus subtilis is known to exhibit
various colony patterns, such as diffusion-limited aggregation (DLA)-like,
compact Eden-like, dense-branching-morphology (DBM)-like,
concentric-ring-like and disk-like, depending on the substrate softness and
nutrient concentration.
We have established the morphological diagram of colony patterns, and examined
and characterized both macroscopically and microscopically
how they grow.
For instance, we have found that there seem to be two kinds of bacterial
cells; active and inactive cells, the former of which drive colony
interfaces outward.
The active cells are particularly distinguished from the inactive ones at
the tips of growing branches of a DBM-like colony as the characteristic
fingernail structure.
We have also found that the concentric-ring-like colony is formed as a
consequence of alternate repetition of advancing and resting of the growing
interface which consists of active cells.
Based on our observations, we have tried to construct a phenomenological but
unified model which produces characteristic colony patterns.
It is a reaction-diffusion type model for the population density of bacterial
cells and the concentration of nutrient.
The essential assumption is that there exist two types of bacterial cells;
active cells that move actively, grow and perform cell division, and
inactive ones that do nothing at all.
We have varied values of the initial nutrient concentration and the ratio of
diffusion rate of bacterial cells to that of nutrients.
They correspond to the specified nutrient concentration in agar plates and
the substrate softness in our experiments, respectively.
Our model is found to be able to globally reproduce all the colony patterns
seen in the experimentally obtained morphological diagram, and is
phenomenologically quite satisfactory.
References
Matsushita M 1997 in Bacteria as Multicellular Organisms
eds. J A Shapiro and M Dworkin (New York: Oxford UP) pp366-393
Matsushita M, Wakita J and Matsuyama T 1995 in Spatio-Temporal Patterns in
Nonequilibrium Complex Systems, Proceedings Volume XXI of Santa Fe Institute
Studies in the Sciences of Complexity, eds. P E Cladis and P Palffy-Muhoray
(Reading: Addison-Wesley) pp609-618
Matsuyama T and Matsushita M 1993 CRC Critical Reviews in Microbiology
19 117
Wakita J, Ràfols I, Itoh H, Matsuyama T and Matsushita M 1998 J. Phys.
Soc. Jpn. 67 3630
Wakita J, Itoh H, Matsuyama T and Matsushita M 1997 J. Phys. Soc. Jpn.
66 67
Matsushita M, Wakita J, Ràfols I, Itoh H, Matsuyama T, Sakaguchi H and
Mimura M 1998 Physica A 249 517
Stochastic resonance
Peter V.E. McClintock
Department of Physics, Lancaster University, UK
Stochastic resonance (SR) is commonly said to occur when a weak
periodic signal in a nonlinear system is enhanced by an increase of the
ambient noise intensity; a stronger definition requires that the
signal/noise ratio (SNR) should also increase. SR has been much
in the news recently, partly on account of its wide occurrence in many
areas of science. After being introduced as a possible explanation of
the earth's ice-age cycle (Benzi et al 1981, Nicolis 1982), SR has
subsequently been observed or invoked in contexts that include lasers
(e.g. McNamara et al 1988), passive optical systems, tunnel diodes, a
Brownian particle in an optical trap, a magnetoelastic ribbon, crayfish
and rat mechanoreceptors, a bistable SQUID (superconducting quantum
interference device), arrays of SR elements, ion channels, magnetic
systems, the El Nino phenomenon, social ills, various types of bistable
electronic model including coexisting periodic attractors, subcritical
bifurcations, systems with thresholds, transient dynamics, a quantum
2-level system, an array of coupled bistable systems, a system driven
by quasimonochromatic (harmonic) noise, excitable neurons, and chemical
systems. There have been several general scientific articles (e.g.
Moss and Wiesenfeld 1995, Bulsara and Gammaitoni 1996) and two largely
complementary topical reviews (Dykman et al 1995, Gammaitoni et al
1998).
We present a succinct introductory review of SR discussing its
physical nature, the insights that can be obtained by treating it as a
linear response phenomenon (Dykman et al, 1990), and the way in which
electronic experiments (Luchinsky et al 1998) have tested the
approximate analytic theory and extended the known range of occurrence
of SR far beyond the systems characterised by static bistable
potentials in which it was originally discovered.
References
Benzi R, Sutera S, and Vulpiani A 1981 J. Phys. A 14
L453
Bulsara A R and Gammaitoni L 1996 Physics Today March 39
Dykman M I, Mannella R, McClintock P V E and Stocks N G 1990
Phys. Rev. Lett. 65 2606
Dykman M I, McClintock P V E, Stein N D and Stocks N G 1992
Phys. Rev. Lett. 68 2718
Dykman M I, Mannella R, McClintock P V E and Stocks N G 1993
Phys. Rev. Lett. 70 874
Dykman M I and McClintock P V E 1998 Nature 391 344
Dykman M I, Haken H, Gang Hu, Luchinsky D G, Mannella R,
McClintock P V E, Ning C Z, Stein N D and Stocks N G 1993 Phys.
Lett. A 180 332
Dykman M I, Luchinsky D G, Mannella R, McClintock P V E, Stein N
D and Stocks N G 1995 Nuovo Cimento D 17 661
Gammaitoni L, Hänggi, Jung P and Marchesoni F 1998
Rev. Mod. Phys. 70 223
Kaufman I Kh, Luchinsky D G, McClintock P V E, Soskin S M and
Stein N D 1998 Phys. Rev. E 57 78
Luchinsky D G, McClintock P V E and Dykman M I 1998 Rep. Prog. Phys.
61 889
McNamara B, Wiesenfeld K and Roy R 1988 Phys. Rev. Lett.
60 2626
Nicolis C 1982 Tellus 34 1
Stocks N G, Stein N D, Soskin S M and McClintock P V E 1992
J. Phys. A: Math. Gen. 25 L1119
Stocks N G, Stein N D and McClintock P V E 1993 J. Phys. A:
Math. Gen. 26 L385
Large fluctuations and optimal paths
Peter V.E. McClintock
Department of Physics, Lancaster University, UK
Most of the interesting and important events that occur in
fluctuating nonlinear dynamical systems, e.g. the transitions between
attractors giving rise to stochastic resonance or transport in Brownian
ratchets, are attributable to large rare fluctuations. Their
analysis requires both evaluation of the probability of the system
occupying a state remote from the attractor and identification of the
fluctuational path through which it reaches that point. Starting from
Boltzmann (1904), a huge body of theory has been developed during this
century; the modern understanding dates from Onsager and Machlup
(1953). But it was not until recently that a method was established
(Dykman et al 1992) by which optimal paths, i.e. the most
probable fluctuational paths, can be measured experimentally.
Recent progress in the area, with particular reference to experiments
on optimal paths in far-from-equilibrium systems, will be discussed.
Like rays in geometrical optics or WKB trajectories in quantum
mechanics, the pattern of optimal paths displays singularities. The
reasons why some of these are physically observable in electronic
experiments, and others are not, will be accounted for though the
topological insights introduced by Dykman et al (1994). Measurements of
an exit location distribution for a noisy nonconservative system
(Luchinsky et al 1999), leading to the observation of saddle-point
avoidance, will be discussed.
References
Arrayás M, Casado J M, Gómez Ordóñez J, McClintock P V E,
Morillo M, Stein N D 1998 Phys. Rev. Lett. 80
2273
Berry M V 1976 Adv. Phys. 25 1
Boltzmann L, 1904 ``On Statistical Mechanics'', address given to
the Scientific Congress in St. Louis, 1904 reprinted in
Theoretical Physics and Philosophical Problems ed B McGuinness
(Dordrecht: Reidel) pp 159-172
Bray A J and McKane A J 1989 Phys. Rev. Lett. 62 493
Chinarov V A, Dykman M I and Smelyanskiy V N 1993
Phys. Rev. E 47 2448
Dykman M I, Krivoglaz M A and Soskin S M 1989 in Noise in
Nonlinear Dynamical Systems ed F Moss and P V E McClintock (Cambridge,
Cambridge University Press) vol. 2 pp 347-380
Dykman M I, McClintock P V E, Stein N D and Stocks N G 1992
Phys. Rev. Lett. 68 2718
Dykman M I, Millonas M M and Smelyanskiy V N 1994 Phys.
Lett. A 195 53
Dykman M I, Luchinsky D G, McClintock P V E and Smelyanskiy V N 1996
Phys. Rev. Lett. 77 5229
Freidlin M I and Wentzell A D 1984 Random Perturbations in
Dynamical Systems (New York: Springer-Verlag).
Graham R 1989 in Noise in Nonlinear Dynamical Systems
edited by F. Moss and P. V. E. McClintock (Cambridge: Cambridge
University Press) vol 1, pp 225-278
Haken H 1975 Rev. Mod. Phys. 47 67
Jauslin H R 1987 J. Stat. Phys. 42 573
Luchinsky D G 1997 J. Phys. A 30 L577
Luchinsky D G and McClintock P V E 1997 Nature 389 463
Luchinsky D G, Maier R S, Mannella R, McClintock P V E and
Stein D L 1997 Phys. Rev. Lett. 79 3109
Luchinsky D G, Maier R S, Mannella R, McClintock P V E and
Stein D L 1999, Phys. Rev. Lett. 82 1806
Maier R S and Stein D L 1996 J. Stat. Phys.
83 291
Onsager L and Machlup S 1953 Phys. Rev. 91 1505-1512
Chaos in economic systems
Erik Mosekilde
Center for Chaos and Turbulence Studies,
Department of Physics,
The Technical University of Denmark, Denmark
The basic assumption in most economic theory is that agents act in
accordance with rational expectations about the future. This implies
that all relevant information supplied to a market is immediately
taken into account, and the noise-like behavior observed in many
economic time series is considered to represent this fast and accurate
adjustment process. Nonetheless, the question remains whether the
concept of efficient markets is consistent with actual economic
conditions. The systematic phase shifts and lags observed between
various economic variables bear evidence of dynamic phenomena with
relatively long adjustment times, and asymmetries in the temporal
variations indicate the presence of nonlinear interactions.
In order to explore the nature of human decision making behavior in
complex, nonlinear systems, we have performed a series of role playing
experiments with a simulated microeconomic system. MIT students of
management and experienced managers from major US companies were asked
to operate a four-stage production distribution chain to ensure a
stable supply of beer. The observed performance was systematically
sub-optimal, leading in many cases to operational costs of more than
ten times the optimal. By virtue of the built-in delays and nonlinear
constraints, most players were unable to ensure a stable operation,
and large-scale fluctuations with characteristic amplitudes and phase
lags developed.
We have formulated a four-parameter anchoring and adjustment
heuristics for the ordering decisions in the game. With
econometrically estimated parameters for each individual participant,
this heuristics is found to reproduce the behavior of the system quite
well. At the same time it explains the sources of poor performance in
the game in term of insufficient levels of inventories, too aggressive
stock adjustments, or inadequate account of supply line variations.
Computer simulations with the estimated ordering heuristics produce
extremely complicated modes of behavior. For many parameter
combinations, including combinations within the range of realistic
policies, the system shows chaotic, hyperchaotic and higher-order
hyperchaotic solutions. It is also possible to observe various forms
of chaos-chaos intermittency.
References
J.S. Thomsen, E. Mosekilde, and J.D. Sterman, Hyperchaotic Phenomena
in Dynamic Decision Making, J. Syst. Analysis and Mod. Simulation 9,
137 (1992)
O. Sosnovtseva and E. Mosekilde, Torus Destruction and Chaos-Chaos
Intermittency in the Beer Model, Int. J. Bifurcation and Chaos 7,
1225 (1997)
E. Mosekilde, Topics in Nonlinear Dynamics: Applications to Physics,
Biology and Economic Systems (World Scientific, Singapore, 1996).
Synchronization of chaotic oscillators
Erik Mosekilde
Center for Chaos and Turbulence Studies,
Department of Physics,
The Technical University of Denmark, Denmark
The ability of interacting, nearly identical chaotic oscillators to
synchronize their motions has been demonstrated for a variety of
different physical, chemical, and biological systems, and applications
for chaos suppression, for monitoring of dynamical systems, and for
different communication purposes are actively being pursued by many
investigators. An interesting question concerns the starting
conditions for which synchronization can be achieved. Other questions
relate to the sensitivity of the synchronized state to a small
parameter mismatch between the interacting oscillators and to the
behavior of the system, once synchronization breaks down.
Riddling of the basin of attraction for the synchronized chaotic state
arises when particular orbits embedded in this state become unstable
to asynchronous perturbations while the state remains attractive on
the average. Under these conditions the neighborhood of any point from
which the trajectories are attracted to the synchronized state will
contain initial conditions that are repelled from it. On-off
intermittency is an extreme form of intermittent bursting that can
sometimes be observed on the other side of the blowout bifurcation
where the synchronized state loses its average attraction.
Considering as a simple example two coupled logistic maps, the lecture
presents three different scenarios for the onset of riddling and for
the subsequent transformations of the basins of attraction. It is
demonstrated how the concepts of absorbing and mixed absorbing areas
play an essential role in explaining the different types of behavior:
The transition from local to global riddling, the distinction between
different types of noise response, and the occurrence of on-off
intermittency. Considering hereafter a system of two coupled
Rössler systems it is shown how similar phenomena arise in time
continuous systems.
References
Yu. Maistrenko, V. Maistrenko, A. Popovich, and E. Mosekilde,
Transverse Instability and Riddled Basins in a System of Two
Coupled Logistic Maps, Phys. Rev. E 57, 2713 (1998)
Yu. Maistrenko, V. Maistrenko, A. Popovich, and E. Mosekilde,
Role of the Absorbing Area in Chaotic Synchronization, Phys.
Rev. Lett. 80, 1638 (1998)
E. Mosekilde, Topics in Nonlinear Dynamics: Applications
to Physics, Biology and Economic Systems (World Scientific, Singapore, 1996).
Chaos in living systems
Erik Mosekilde
Center for Chaos and Turbulence Studies,
Department of Physics,
The Technical University of Denmark, Denmark
Physiological control systems offer one of the most interesting areas
of application for nonlinear dynamics. Complementary to the concept of
homeostasis that has dominated physiological thinking for such a long
time, unstable phenomena are increasingly being recognized as
significant for the regulation and function of normal physiological
systems. Many hormonal systems, for instance, operate in a pulsatile
mode with the release of insulin, growth hormone and luteinizing
hormone typically occurring with one-three hour intervals.
By regulating the excretion of salts and water the kidneys play an
important role in regulating the arterial blood pressure. To protect
their own function and secure a relatively constant supply of blood,
the kidneys also dispose of mechanisms that can compensate for
variations of the arterial pressure. This ability rests at least
partly with controls in the individual nephron, primarily the
so-called tubuloglomerular feedback (TGF). This is a negative feedback
that adjusts the diameter of the incoming arteriole in response to
variations in the chloride concentration of the fluid that leaves the
nephron.
Experiments on rat kidneys performed at The Department of Medical
Physiology, University of Copenhagen have demonstrated that the time
delays associated with the TGF mechanism tend to produce oscillations
in the nephron pressure and flow regulation with a typical period of
20-30 sec. For rats with elevated blood pressure, the oscillations are
often chaotic. Moreover, both regular and chaotic oscillations can be
observed to synchronize between neighboring nephrons.
The lecture presents a detailed physiological model of the feedback
controls of the individual nephron. A bifurcation analysis of this
model reveals the existence of so-called crossroad structures of
overlapping saddle-node and period-doubling bifurcations that can
explain the experimental observations. The model is subsequently
extended to consider the coupling between two neighboring nephrons
that share the same afferent arteriole. The coupled nephron model
reveals a variety of different synchronization phenomena including
in-phase and anti-phase synchronization of regularly oscillating
nephrons and complete and partial synchronization of chaotic nephrons.
References
M. Barfred, E. Mosekilde, and N.-H. Holstein-Rathlou, Bifurcation
Analysis of Nephron Pressure and Flow Regulation, Chaos 6, 280 (1996)
J. Sturis et al., Phase-Locking Regions in a Forced Model of Slow
Insulin and Glucose Oscillations, Chaos 5, 193 (1995)
E. Mosekilde, Topics in Nonlinear Dynamics: Applications to Physics,
Biology and Economic Systems (World Scientific, Singapore, 1996).
Asymptotic expansions beyond all orders: asymptotic description
of chaotic dynamics
Katsuhiro Nakamura and Hiroyuki Kushibe
and Hiroyuki Kushibe
 Department
of Applied Physics, Osaka City University, Osaka, Japan
Department
of Applied Physics, Osaka City University, Osaka, Japan
 Department
of Applied Biochemistry, Osaka City University, Osaka, Japan
Department
of Applied Biochemistry, Osaka City University, Osaka, Japan
Heteroclinic or homoclinic structures are the well-known mechanism for a
genesis of chaos in conservative dynamical systems. While numerical
iterations of low-dimensional maps easily provide these complicated
structures, it is very difficult to derive them analytically, as addressed
by Poincaré more than a century ago.
However, the difficulty can now be overcome by using a scheme of
the asymptotic expansions beyond all orders. The scheme was recently
sharpened with a help of the theoretical tool of Borel summability and
Stokes phenomena. The pioneering works by Hakim and Mallick(1993)
and Gelfreich et al(1994) exploited the asymptotics beyond all orders
to elucidate the angle of separatrices splitting of the standard map.
It is highly desirable to develop the scheme further to describe the
chaotic dynamics, i.e., the stretching and folding of the unstable manifold
impinging upon the hyperbolic fixed point. Tovbis et al (1998),
Nakamura and Hamada(1996) and Nakamura (1997) attempted to describe
analytically the chaotic dynamics for the Henon and cubic maps. However,
they failed to derive the Stokes multiplier precisely. In order to overcome
this problem, some new systematic approach should be invented.
In this talk, dealing with the standard and cubic maps., i.e.,
time-discrete dynamical systems with cosine and double-well potentials,
respectively, we shall provide an asymptotic analytical description of the
complicated heteroclinic and homoclinic structures on extremely fine
scales and compare the issue with that of an exact numerical iteration of
the maps. Technical problems around the Borel summability and Stokes
phenomena are also discussed in detail. The talk is based on the
latest work by Nakamura and Kushibe (1999).
References
Gelfreich V G, Lazutkin V F and Svanidze N V 1994
Physica D 71 82
Hakim V and Mallick K 1993 Nonlinearity 6 57.
Nakamura K 1997 Quantum versus Chaos: Questions emerging from
Mesoscopic Cosmos (Dordrecht: Kluwer Academic).
Nakamura K and Hamada M 1996 J. Phys.A 29 7315;
Nakamura K and Kushibe H 1999, preprint.
Tovbis A , Tsuchiya M and Jaffe C 1998 Chaos 8 665.
Semiclassical theory of
mesoscopic 3-dimensional billiards:
orbital magnetism and persistent current
Jun Ma and Katsuhiro Nakamura
Department of Applied Physics, Osaka City University, Osaka, Japan
In the mesoscopic billiards, chaos is known to play an important role in
the orbital diamagnetism as pointed out by Nakamura(1993). While subsequent
papers by Oppen(1994) and Richter et al(1996) dealt with mesoscopic 2-d
billiards from the semiclassical viewpoint, quite few works have appeared
about the rich phenomena in orbital diamagnetism of 3-d billiards.
In this talk, the magnetic susceptibility of ballistic 3-d billiards is
investigated on the basis of the independent-electron model, for both
single-billiard and ensemble-averaged cases. Using a semiclassical method,
three kind of 3-d billiards subjected to weak uniform magnetic field are
analyzed: spherical shell billiards; chaotic 3-d billiards but having SO(2)
rotational symmetry; completely chaotic 3-d billiards without any
continuous symmetry. We particularly elucidate the role of geometric
symmetry in the susceptibility. According to different symmetries,
different trace formulas (e.g., the Gutzwiller trace formula extended
so as to incorporate continuously-degenerate periodic orbits) are exploited.
We first calculate the magnetic susceptibility for a spherical shell
at finite temperature. Periodic orbits lying on great circular planes that
share the center with both of the inner and outer spherical shells give
rise to the susceptibility. The obtained result is compared with the
corresponding results for a SO(2) rotational-symmetric chaotic billiard
and for a completely chaotic 3-d billiard. Furthermore, the asymmetry
in the magnetic response is found for 3-d billiard with SO(2) symmetry.
The analysis is also made on the persistent current in the
corresponding three kinds of 3-d ``shell" billiards. The talk is based on
the latest works by Ma and Nakamura (1999).
References
Ma J and Nakamura K, preprints 1&2.
Nakamura K 1993 Quantum Chaos: a New Paradigm of Nonlinear Dynamics
(Cambridge: Cambridge University Press).
Richter K et al 1996 Phys. Rep. 276 1.
von Oppen F 1994 Phys. Rev. B 50 17151.
Quantum mesoscopic systems:
I. Random matrix theory of the conductance of a chaotic cavity
Jean-Louis Pichard
CEA Saclay, Service de Physique de l'Etat Condensé,
91191 Gif sur Yvette cedex, France
In this first lecture, the conductance of a ballistic quantum dot
(having classical chaotic dynamics and being coupled by ballistic
point contacts to two electron reservoirs) will be described on the
single assumption that its scattering matrix is a member of Dyson's
circular ensemble. The weak-localization corrections to the average
conductance and the universal amplitude of the conductance fluctuations
will be calculated. This example will show how the methods of random
matrix theory can be implemented for describing quantum transport
when the electron-electron interaction remains negligible (non interacting
quasi-particles). The results discussed in this lecture have been published
in Jalabert, Pichard and Beenakker (1994) and in Baranger and
Mello (1994). Reviews for the random matrix theory of quantum transport
can be found in Pichard (1991), Stone, Mello, Muttalib and Pichard (1991),
Beenakker (1997) and Guhr, Müller-Groeling, and Weidenmüller (1998).
References
R.A. Jalabert, J.-L. Pichard and C.W.J. Beenakker, 1994,
Europhys. Lett. 27, 255.
H. Baranger and P.A. Mello, 1994, Phys. Rev. Lett.
73, 142.
J.-L. Pichard, 1991, in Quantum coherence in Mesoscopic Systems,
B. Kramer ed, NATO-ASI Series B, Physics Vol 254, 369-400.
A.D. Stone, P.A. Mello, K.A. Muttalib and J.-L. Pichard, 1991, in
Mesoscopic Phenomena in Solids eds. B.L. Altshuler, P.A. Lee and
R.A. Webb (Amsterdam: North-Holland), 369-449.
C.W.J. Beenakker, 1997, Rev. of Modern Phys. 69,731.
T. Guhr, A. Müller-Groeling and H. Weidenmüller, 1998,
Phys.Rep. 299, 189.
Quantum mesoscopic systems:
II. Chaotic mixing of the one body states by
electron-electron interactions and delocalization in one dimension.
Jean-Louis Pichard
CEA Saclay, Service de Physique de l'Etat Condensé,
Gif sur Yvette, France
The effect of electron-electron interactions when the one body states
are localized will be introduced in a simple limit: two interacting
particles (TIP) in a disordered chain. This problem was introduced
by Shepelyansky (1994) and has been studied by Pichard et al (1996-1998).
The TIP localization length will be estimated and the TIP spectral
statistics will be discussed. The strength of the interaction leading
to a maximum mixing of the one body states and to a maximum enhancement
of the TIP localization length will be derived. Then, we will consider
the ground state properties of a finite density of spinless fermions with
short range interactions in a disordered chain. The enhancement of the
persistent current driven by an Aharonov-Bohm flux when the system is
between the Anderson (no interaction) and the Mott limits (correlated array
of charges for strong interaction) will be discussed following Schmitteckert
et al (1998).
References
D. L. Shepelyansky, 1994, Phys. Rev. Lett. 73, 2607.
D. Weinmann and J.-L. Pichard, 1996, Phys. Rev. Lett.
77, 1556.
X. Waintal and J.-L. Pichard, 1999, Eur. Phys. J. B6, 117.
X. Waintal, D. Weinmann and J.-L. Pichard, 1999, Eur. Phys. J
B7, 451.
X. Waintal, S. de Toro-Arias and J.-L. Pichard, 1999, Eur. Phys. J
B, in press.
P. Schmitteckert, R. Jalabert, D. Weinmann and J.-L. Pichard, 1998,
Phys. Rev. Lett. 81, 2308.
Quantum mesoscopic systems:
III. Two dimensional gases of charges with Coulomb repulsions:
A new metal between the Fermi glass and the Wigner crystal.
Jean-Louis Pichard
CEA Saclay, Service de Physique de l'Etat Condensé,
Gif sur Yvette, France
The ground state and the low energy excitations of electron (or hole)
gases confined in a two dimensional random potential are the subject
of this third lecture. Without interaction, one cannot have
a two dimensional metal according to the scaling theory of localization.
Experiments pioneered by Kravchenko et al (1994) (and nowadays confirmed
by many others experimental groups) have given evidences for unexpected
insulator-metal transitions. We will review the results obtained by numerical
studies of small clusters: When the Coulomb energy to Fermi energy ratio
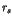 is small, the system is an Anderson insulator while one has a pinned
Wigner crystal in the large
is small, the system is an Anderson insulator while one has a pinned
Wigner crystal in the large 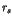 limit. For intermediary
limit. For intermediary 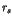 , there are
growing numerical (Benenti et al 1999) and experimental evidences supporting
the existence of a new metal with an ordered flow of enhanced persistent
currents.
, there are
growing numerical (Benenti et al 1999) and experimental evidences supporting
the existence of a new metal with an ordered flow of enhanced persistent
currents.
References
S.V. Kravchenko, G.V. Kravchenko, J.E. Fourneaux, J.E. Pudalov
and M. D'Iorio, 1994 Phys. Rev. B 50, 8038.
G. Benenti, X. Waintal and J.-L. Pichard, 1999, cond-mat/ 9904096.
G. Benenti, X. Waintal, J.-L. Pichard and D.L. Shepelyansky, 1999,
cond-mat/ 9903339.
Integrability and transport in quantum many body systems
Peter Prelovšek
Faculty of Mathematics and Physics, and J. Stefan Institute,
Ljubljana, Slovenia
The particle transport in macroscopic many-fermion quantum systems at
finite temperatures will be discussed. It will be argued that there is
a fundamental difference between the integrable and nonintegrable
systems [1]. Even when the current is not a conserved quantity the
integrable models show a dissipationless transport, they can in fact
behave as ideal conductors in the metallic regime and as ideal
insulators in the insulating regime, while nonintegrable systems are
expected to behave as generic conductors or resistors [2]. In this
connection the role of conservation laws will be pointed out [3] and a
relation to the level statistics will be examined.
References
[1] H. Castella, X. Zotos, and P. Prelovšek, Phys. Rev. Lett.
74, 972 (1995).
[2] X. Zotos and P. Prelovšek, Phys. Rev. B 53, 983
(1996).
[3] X. Zotos, F. Naef, and P. Prelovšek, Phys. Rev. B 55, 11029
(1997).
Quantum Poincaré mapping
Tomaz Prosen
Physics Department, Faculty of Mathematics and Physics,
University of Ljubljana, Slovenia
The lecture will give a review of the recent theoretical work
on the quantization of Poincaré mapping on the surface of section
(SOS) of general bounded and autonomous Hamiltonian systems.
We will begin, historically, to describe the semi-classical
construction by Bogomolny [1] of the approximate quantum
Poincaré mapping (QPM). Then we will
formulate the scattering approach to quantization, which has been
introduced for billiards by Smilansky et al [2], and which can be
reinterpreted as an approach to exact quantization on SOS. We will
show [3] that one can generally construct the exact QPM
 , as the product of two
scattering operators
, as the product of two
scattering operators
 of the associated scattering
problems which are obtained by amputing upper/lower half of configuration
space along the configurational SOS and attaching a semi-infinite flat
`wave-guide' instead. Although this form of QPM enables one to write an exact
quantization condition (QC) as
of the associated scattering
problems which are obtained by amputing upper/lower half of configuration
space along the configurational SOS and attaching a semi-infinite flat
`wave-guide' instead. Although this form of QPM enables one to write an exact
quantization condition (QC) as
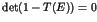 and has the correct
semi-classical limit of Bogomolny (as
and has the correct
semi-classical limit of Bogomolny (as
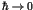 ), it has
a disadvantage of not being strictly unitary operator, so it does not
conserve probability,
and hence, strictly speaking, it cannot be interpreted as
an evolution operator on SOS.
However, we propose a simple and almost unique technique of
unitarization of QPM [4]
), it has
a disadvantage of not being strictly unitary operator, so it does not
conserve probability,
and hence, strictly speaking, it cannot be interpreted as
an evolution operator on SOS.
However, we propose a simple and almost unique technique of
unitarization of QPM [4]
 ,
which yields the strictly unitary QPM
,
which yields the strictly unitary QPM 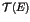 on the Hilbert
space of
on the Hilbert
space of 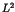 functions over the configurational SOS
(which has one degree of freedom less than the full space problem),
and which at the same time preserves (i) the (semi)classical limit,
as well as (ii) the exact QC, namely,
functions over the configurational SOS
(which has one degree of freedom less than the full space problem),
and which at the same time preserves (i) the (semi)classical limit,
as well as (ii) the exact QC, namely,
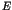 is an eigenenergy iff
is an eigenenergy iff
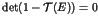 ,
or alternatively, iff one of the eigenphases
,
or alternatively, iff one of the eigenphases 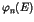 of the
unitary QPM
of the
unitary QPM 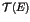 crosses zero,
crosses zero,
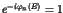 .
The theoretical ideas will be worked out explicitly on an example of
a semi-separable system (Prosen 1996), a simple two-degree-of-freedom
dynamical system which is separable above and below SOS, but is
discontinuous on SOS, hence in full space it is non-separable, non-integrable
and possibly chaotic (depending on parameters).
.
The theoretical ideas will be worked out explicitly on an example of
a semi-separable system (Prosen 1996), a simple two-degree-of-freedom
dynamical system which is separable above and below SOS, but is
discontinuous on SOS, hence in full space it is non-separable, non-integrable
and possibly chaotic (depending on parameters).
References
(1) Bogomolny E B 1992 Nonlinearity 5 805;
1990 Comments At.Mol.Phys. 25 67
(2) Doron E and Smmlansky U 1992 Nonlinearity 5 1055,
Dietz B and Smilansky U 1993 Chaos 3 581,
Schanz H and Smilansky U 1995 Chaos, Solitons & Fractals 5 1289
(3) Prosen T 1995 J. Phys. A: Math. Gen. 28 4133;
1994 J. Phys. A: Math. Gen. 27 L709;
1997 Open Sys.& Information Dyn. 4 339
(4) Prosen T 1996 Physica D 91 244;
1995 J. Phys. A: Math. Gen. 28 L349
Quantum chaos, ergodicity and mixing in
generic many-body systems in thermodynamic limit
Tomaz Prosen
Physics Department, Faculty of Mathematics and Physics,
University of Ljubljana, Slovenia
We address an old unsolved problem of (quantum) statistical
mechanics, namely the justification of the ergodic hypothesis,
and consequently, the `derivation' or dynamical understanding of
macroscopic statistical laws, e.g. the transport laws such as Ohm's, Fourier's
or Fick's law, from the (non-integrable) microscopic equations of motion.
To this end we propose to study (i) the dynamics (direct time-evolution),
and (ii) the existence of dynamical conservation laws (integrals of motion),
of simple quantum-many body dynamical system for which thermodynamic
limit can be approached numerically. This we do (1)
by means of efficient (and presumably novel) numerical methods,
namely, by (i) multi-dimensional (anti)symmetrized Fast Fourier
Transformation, and (ii) solving Galerkin-like variational problems in
truncated operator Hilbert spaces of quantum observables of an
infinite many-body system, respectively.
We define (1) a generic but simple non-integrable quantum
many-body system of locally interacting particles, namely a
kicked  model of spinless fermions on 1-dim lattice (equivalent to a
kicked Heisenberg XX-Z spin
model of spinless fermions on 1-dim lattice (equivalent to a
kicked Heisenberg XX-Z spin chain). Statistical properties of
dynamics (quantum ergodicity, quantum mixing (2)) and the nature of
quantum transport in thermodynamic limit are considered as the kick
parameters (which control the degree of non-integrability) are varied.
We find and demonstrate ballistic transport
and non-ergodic, non-mixing dynamics (implying infinite conductivity at
all temperatures) in the integrable regime of zero or very small kick
parameters (as conjectured already in (3)), and more generally and
important, also in non-integrable regime of intermediate values
of kicked parameters, whereas only for sufficiently large kick parameters we
recover quantum ergodicity and mixing implying normal (diffusive) transport.
Based on numerical results we propose a (dynamical) phase transition
with an order parameter
chain). Statistical properties of
dynamics (quantum ergodicity, quantum mixing (2)) and the nature of
quantum transport in thermodynamic limit are considered as the kick
parameters (which control the degree of non-integrability) are varied.
We find and demonstrate ballistic transport
and non-ergodic, non-mixing dynamics (implying infinite conductivity at
all temperatures) in the integrable regime of zero or very small kick
parameters (as conjectured already in (3)), and more generally and
important, also in non-integrable regime of intermediate values
of kicked parameters, whereas only for sufficiently large kick parameters we
recover quantum ergodicity and mixing implying normal (diffusive) transport.
Based on numerical results we propose a (dynamical) phase transition
with an order parameter 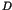 (charge stiffness, which is the time-averaged
current auto-correlation function) from non-ergodic and
non-mixing quantum dynamics (ordered phase,
(charge stiffness, which is the time-averaged
current auto-correlation function) from non-ergodic and
non-mixing quantum dynamics (ordered phase, 
 0)
to ergodic and mixing dynamics (disordered phase,
0)
to ergodic and mixing dynamics (disordered phase,  = 0 ) in the
thermodynamic limit.
Similarity with order-to-chaos transition of generic non-integrable
one-particle quantum systems in semi-classical limit is striking,
and we mention a result (4) on close formal
relation between dynamics of a particular class of non-linear quantum
many body systems (in thermodynamic limit) and an associated class of
one-body quantum systems (in classical limit).
= 0 ) in the
thermodynamic limit.
Similarity with order-to-chaos transition of generic non-integrable
one-particle quantum systems in semi-classical limit is striking,
and we mention a result (4) on close formal
relation between dynamics of a particular class of non-linear quantum
many body systems (in thermodynamic limit) and an associated class of
one-body quantum systems (in classical limit).
References
(1) Prosen T 1998 Phys. Rev. Lett. 80 1808;
1998 J. Phys. A: Math. Gen. 31 L645;
1998 `Ergodic properties of a generic non-integrable quantum many-body
system in thermodynamic limit', preprint cond-mat/9808150
(2) Jona-Lasinio G and Presilla C 1996 Phys. Rev. Lett.
77 4322.
(3) Castella H, Zotos X, and Prelovšek P 1995 Phys. Rev. Lett.
74 972;
Zotos X and Prelovšek P, 1996 Phys. Rev. B 53 983;
Zotos X, Naef F, and Prelovšek P 1997 Phys. Rev. B 55 11029
(4) Prosen T 1998 `A Map from 1d Quantum Field Theory to Quantum Chaos on a
2d Torus', preprint cond-mat/9809211
Chaotic dynamics and statistical mechanics in Hamiltonian
systems with many degrees of freedom
Andrea Rapisarda
Dipartimento di Fisica, Universitá di Catania,
and
Istituto Nazionale
di Fisica Nucleare, Sezione di Catania, Italy
We discuss the connection between chaotic dynamics
and equilibrium statistical mechanics in systems
with many degrees of freedom.
The talk will focus in particular on the links between
microscopic chaos and phase transitions
in the Hamiltonian Mean Field model (HMF), Antoni and Ruffo (1995).
The latter is a simple toy model of
 fully-coupled rotators which shows a second order phase transition.
Recently
the equilibrium properties and the dynamical behavior of HMF
have been investigated numerically and analytically in several papers
by Latora, Rapisarda and Ruffo (1998),(1999) . Our main result is that
both the largest Lyapunov exponent and Kolmogorov-Sinai entropy
show a peak at the critical energy
fully-coupled rotators which shows a second order phase transition.
Recently
the equilibrium properties and the dynamical behavior of HMF
have been investigated numerically and analytically in several papers
by Latora, Rapisarda and Ruffo (1998),(1999) . Our main result is that
both the largest Lyapunov exponent and Kolmogorov-Sinai entropy
show a peak at the critical energy 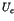 .
This result is checked to be valid in the limit
.
This result is checked to be valid in the limit 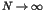 .
Scale law behaviors for the Lyapunov exponents are derived, and an
important link between chaoticity and the
thermodynamical fluctuations, expressed by kinetic energy
fluctuations or specific heat, is found.
The canonical thermodynamical Vlasov solution has been successfully checked
in numerical simulations. In general, chaotic dynamics provides the mixing
property in phase space necessary for obtaining equilibration. However
relaxation to equilibrium can be very slow and grows with
.
Scale law behaviors for the Lyapunov exponents are derived, and an
important link between chaoticity and the
thermodynamical fluctuations, expressed by kinetic energy
fluctuations or specific heat, is found.
The canonical thermodynamical Vlasov solution has been successfully checked
in numerical simulations. In general, chaotic dynamics provides the mixing
property in phase space necessary for obtaining equilibration. However
relaxation to equilibrium can be very slow and grows with  close to the critical point where metastable states are found.
Possible connection to anomalous
transport properties and Levy walks will be discussed in connection
to the out-of-equilibrium regime.
Our results seem to be very general
and confirm a previous pioneering work by Bonasera, Latora and Rapisarda
1995. Lately similar features have been
found also in other models by Caiani et al (1998),
Anteneodo and Tsallis (1998),
Torcini and Antoni (1999).
The results discussed for this toy model can be very useful
in order to understand the multifragmentation phase transition
in excited nuclei, Atalmi et al (1998), and clusters ,
Farizon et al (1998), and could be important
also in astrophysics for
autogravitating systems, Yawn and Miller
(1997).
In general this new scenario provides an interesting bridge
between Hamiltonian chaos in systems with many degrees of freedom
and statistical mechanics.
close to the critical point where metastable states are found.
Possible connection to anomalous
transport properties and Levy walks will be discussed in connection
to the out-of-equilibrium regime.
Our results seem to be very general
and confirm a previous pioneering work by Bonasera, Latora and Rapisarda
1995. Lately similar features have been
found also in other models by Caiani et al (1998),
Anteneodo and Tsallis (1998),
Torcini and Antoni (1999).
The results discussed for this toy model can be very useful
in order to understand the multifragmentation phase transition
in excited nuclei, Atalmi et al (1998), and clusters ,
Farizon et al (1998), and could be important
also in astrophysics for
autogravitating systems, Yawn and Miller
(1997).
In general this new scenario provides an interesting bridge
between Hamiltonian chaos in systems with many degrees of freedom
and statistical mechanics.
References
Anteneodo C and Tsallis C 1998
Phys. Rev. Lett 80 5313
Antoni M and Ruffo S 1995 Phys. Rev. E 52
2361
Atalmi A, Baldo M, Burgio G F and Rapisarda A 1998 Phys. Rev.
C 58 2238
Bonasera A, Latora V and Rapisarda A 1995
Phys. Rev. Lett. 75
3434
Caiani L, Casetti L, Clementi C and Pettini G, Pettini M and Gatto R
1998 Phys. Rev. E 57 3886
Farizon B et al 1998
Phys. Rev. Lett. 81
4108
Latora V, Rapisarda A and Ruffo S 1998 Phys. Rev. Lett. 80
698
Latora V, Rapisarda A and Ruffo S 1999 Physica D
in press, chao-dyn/9803019
Torcini A and Antoni M 1999
Phys. Rev. E in press, cond-mat/9808068
Yawn K R and Miller B N 1997
Phys. Rev. Lett. 79
3561
Chaos in quantum transport:
From electron billiards to Coulomb blockade
Klaus Richter
Max-Planck-Institut für Physik komplexer Systeme,
Dresden, Germany
We review aspects of classical and quantum transport through
electronic mesoscopic systems. In the first part of the talk
we discuss properties of open conductors which represent
realizations of non-interacting chaotic quantum billiards. We
introduce semiclassical concepts
which allow us to relate quantum coherence effects in the
conductance to properties of classical irregular scattering
in these billiards (Baranger et al. 1993, Stone 1995, Richter 1999).
We highlight the achievements of these
approaches for the understanding of related recent experiments
on transport through semiconductor nanostructures.
We furthermore discuss problems of the standard semiclassical
transport theory to account adequately for weak localization,
a quantum correction to the average conductance,
in ballistic systems. We outline new theoretical advances
which may cope with these problems and introduce the concept
of the Ehrenfest time in the context of
chaotic transport (Aleiner and Larkin 1996).
These approaches enable us
to extract from the quantum weak localization
correction the mean Liapunov exponent of the
classical counterpart of a ballistic mesoscopic
system (Yevtushenko et al. 1999).
Upon reducing the coupling of the quantum dot (billiard) to the
leads, interaction effects become important (Kastner 1992). In the second part
of the talk we thus describe novel interaction phenomena
in this Coulomb blockade regime; namely strong fluctuations
in the conductance-peak heights and spacings. (Experimentally)
observed fluctuations in the related ground state energies do not follow
Wigner-Dyson (GOE- or GUE-) statistics
(Sivan et al. 1996, Simmel et al. 1999)
and call for refined random
matrix approaches and a more careful consideration of level
statistics of interacting electrons in chaotic quantum dots.
We review recent theoretical approaches and discuss in particular
the interplay between electron-electron interactions and the
confinement geometry (integrable/chaotic) of ballistic quantum dots.
We do this
on the basis of both exact diagonalization for few particles and
self-consistent Hartree-Fock calculations for a larger number of electrons.
References
Baranger, H.U., R.A. Jalabert, and A.D. Stone, Chaos 3, 665 (1993).
Stone, A.D. in Mesoscopic Quantum Physics,
edited by E. Akkermans, G. Montambaux, J.-L. Pichard, and J.
Zinn-Justin (Elsevier, New York, 1995).
Richter, K., Semiclassical Theory of Mesoscopic Quantum Systems,
Springer Tracts in Modern Physics, in print (1999).
Aleiner I.L. and A.I. Larkin, Chaos, Solitons & Fractals 8, 1179
(1997).
Oleg Yevtushenko, Gerd Lütjering, Dieter Weiss, and
Klaus Richter, preprint MPIPKS-9902004 (1999).
Kastner, M., Rev. Mod. Phys. 64 849 (1992).
Sivan, U.,
R. Berkovits, Y. Aloni, O. Prus, A. Auerbach and G. Ben-Yosef,
Phys. Rev. Lett. 77, 1123 (1996).
Simmel, F., D. Abusch-Magder, D.A. Wharam, M.A. Kastner,
and J.P. Kotthaus (cond-mat 9901274).
Topics in quantum chaos of generic systems I & II
Marko Robnik
Center for Applied Mathematics and Theoretical Physics,
University of Maribor, Maribor, Slovenia
We review the main ideas and results in the
stationary problems of quantum chaos in generic (mixed) systems,
whose classical dynamics has regular (invariant tori) and
chaotic regions coexisting in the phase space. First we
discuss the universality classes of spectral fluctuations
(GOE/GUE for ergodic systems, and Poissonian for integrable
systems). We explain the problems in the
calculation of the invariant (Liouville) measure of
classically chaotic components, which has recently been
studied by Robnik et al (1997) and by Prosen and Robnik (1998).
Then we describe the Berry-Robnik (1984) picture,
which is claimed to become exact in the strict semiclassical
limit
 .
However, at not sufficiently small values of
.
However, at not sufficiently small values of 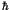 we see
a crossover regime due to the localization properties of
stationary quantum states where Brody-like behaviour with
the fractional power law level repulsion is observed in
the corresponding quantal energy spectra.
we see
a crossover regime due to the localization properties of
stationary quantum states where Brody-like behaviour with
the fractional power law level repulsion is observed in
the corresponding quantal energy spectra.
References
Aurich R, Bäcker A and Steiner F 1997 Int. J. Mod. Phys. 11
805
Berry M V 1983 in Chaotic Behaviour of Deterministic Systems
eds. G Iooss, R H G Helleman and R Stora (Amsterdam: North-Holland)
pp171-271
Berry M V 1991 in Chaos and Quantum Physics eds.
M-J Giannoni, A Voros and J Zinn-Justin (Amsterdam: North-Holland)
pp251-303
Berry M V and Robnik M 1984 J. Phys. A: Math. Gen. 17 2413
Bohigas O 1991 in Chaos and Quantum Physics eds.
M-J Giannoni, A Voros and J Zinn-Justin (Amsterdam: North-Holland) pp87-199
Bohigas O, Giannoni M.-J. and Schmit C 1984 Phys. Rev. Lett.
25 1
Casati G and Chirikov B V 1994 in Quantum Chaos: Between Order and
Disorder eds. G. Casati and B.V. Chirikov (Cambridge: Cambridge University
Press)
Guhr T, Müller-Groeling A and Weidenmüller H A 1998,
Phys.Rep. 299 189
Li Baowen and Robnik M 1994 J. Phys. A: Math. Gen. 27 5509
Li Baowen and Robnik M 1995a J. Phys. A: Math. gen. 28 2799
Li Baowen and Robnik M 1995b J. Phys. A: Math. gen. 28 4843
Prosen T and Robnik M 1993a J. Phys. A: Math. Gen. 26 L319
Prosen T and Robnik M 1993b J. Phys. A: Math. Gen. 26 1105
Prosen T and Robnik M 1993c J. Phys. A: Math. Gen. 26 2371
Prosen T and Robnik M 1993d J. Phys. A: Math. Gen. 26 L37
Prosen T and Robnik M 1994a J. Phys. A: Math. Gen. 27 L459
Prosen T and Robnik M 1994b J. Phys. A: Math. Gen. 27 8059
Robnik M and Prosen T 1997 J. Phys. A: Math. Gen. 30 8787
Robnik M 1984 J. Phys. A: Math. Gen. 17 1049
Robnik M 1988 in "Atomic Spectra and Collisions in External Fields", eds.
K T Taylor, M H Nayfeh and C W Clark, (New York: Plenum) pp265-274
Robnik M 1998 Nonlinear Phenomena in Complex Systems 1 1
Chaotic Jung scattering maps versus topological chaos of the
Hamiltonian flow
Thomas H. Seligman
Centro Internacional de Ciencias
and Centro de Ciencias Físicas, University of Mexico, UNAM,
Cuernavaca, México
The classical scattering map proposed by Jung is the classical
analog of the quantum S-matrix. It therefore contains the
information we can obtain by asymptotic measurement for a classical
scattering system. A detailed analysis of the relation of
integrability and chaos for the Jung map and the Hamiltonian flow
shows that the connection is complicated and dependent of the choice
of the ``unperturbed Hamiltonian'' 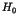 . For the typical choice
of
. For the typical choice
of 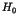 , namely the free particle, we can readily construct
examples where the flow is integrable, but the scattering map is
chaotic. This is due to the incompatibility of the integrals of
motion of the Hamiltonian
, namely the free particle, we can readily construct
examples where the flow is integrable, but the scattering map is
chaotic. This is due to the incompatibility of the integrals of
motion of the Hamiltonian 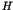 with those of
with those of 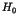 . To transfer
the integrability of
. To transfer
the integrability of 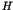 to the integrability of the
Jung map it is necessary and sufficient that
to the integrability of the
Jung map it is necessary and sufficient that 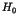 conserves at
least asymptotically the integrals of motion of
conserves at
least asymptotically the integrals of motion of 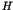 .
This implies that it is not particularly simple to distinguish chaos
or integrability from scattering functions. Some simple examples
illustrate that selfsimilar and even fractal structures in the
scattering functions may result from integrable Hamiltonians.
We may pass from classical to quantum mechanics if we realize that the Jung
map is a canonical map of channel space (considered as a symplectic
manifold or phase space) onto itself and that the
S-matrix is the unitary representation of this map. This implies
that the integrability properties of this map determine those of the
S-matrix. The criteria of integrability carry over easily to the
quantum case.
There is a further interesting aspect that results from the
interpretation of the S-matrix as a representation of the Jung map.
The statistical properties of the spectrum of the S-matrix
not determined by integrability or chaos in the
Hamiltonian flow, but rather by the corresponding properties of the
Jung map. This can be understood in terms of a series of arguments
centered around the concept of structural invariance, which
establish the connection between chaos and random matrix
theory; This connection is based on a probabilistic argument which
allows for all the exceptions and special cases that exist in this context.
It is short of being a proof because the existence of an invariant
measure on the group of invertible canonical transformations has to be
established.
.
This implies that it is not particularly simple to distinguish chaos
or integrability from scattering functions. Some simple examples
illustrate that selfsimilar and even fractal structures in the
scattering functions may result from integrable Hamiltonians.
We may pass from classical to quantum mechanics if we realize that the Jung
map is a canonical map of channel space (considered as a symplectic
manifold or phase space) onto itself and that the
S-matrix is the unitary representation of this map. This implies
that the integrability properties of this map determine those of the
S-matrix. The criteria of integrability carry over easily to the
quantum case.
There is a further interesting aspect that results from the
interpretation of the S-matrix as a representation of the Jung map.
The statistical properties of the spectrum of the S-matrix
not determined by integrability or chaos in the
Hamiltonian flow, but rather by the corresponding properties of the
Jung map. This can be understood in terms of a series of arguments
centered around the concept of structural invariance, which
establish the connection between chaos and random matrix
theory; This connection is based on a probabilistic argument which
allows for all the exceptions and special cases that exist in this context.
It is short of being a proof because the existence of an invariant
measure on the group of invertible canonical transformations has to be
established.
References
C. Jung, J. Phys. 19 (1986) 1345
C. Jung, T.H. Seligman Phys Rep Int. J. Mod. Phys. 11
(1997) 805
C. Jung, C. Mejía and T.H. Seligman, Phys. Lett. A 198 (1995) 306
T.H. Seligman, Proceedings Wigner Symposium; Goslar 1991
(World Scientific, Singapur,) (1992);
T.H. Seligman, Quantum Chaos
Eds. G.Casati and B. Chirikov
Cambridge University Press 1995 p. 577;
F. Leyvraz and T.H. Seligman,
Phys Lett. A 168, (1992), 348-352
Unitary quantum Poincaré maps and Rydberg molecules
Thomas H. Seligman
Centro Internacional de Ciencias
and Centro de Ciencias Físicas, University of Mexico, UNAM,
Cuernavaca, México
Multichannel quantum defect theory (MQDT) has proven very successful for the
calculation of Rydberg molecules. This theory uses results from scattering
theory to obtain information about states near, but below threshold.
In a particular approximation for the classical system, Lombardi showed
that MQDT provides the exact quantum solution.
As this approximate system may be characterized by a symplectic or
canonical map, MQDT can find a much more transparent interpretation
as a unitary representation of this map. A more careful analysis
shows that indeed MQDT is a true quantum Poincaré map (QPM). Remember that
Bogomolny's definition of a QPM is semi-classical. By consequence the map
becomes
unitary only in the limit 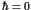 .
Prosen has proposed a very elegant unitarization of the QPM at the
price of obtaining an infinite dimensional matrix.
In our case the QPM is constructed directly from unitary transformations
between body fixed and space fixed frames as well as the phase shifts
typical of MQDT, thus yielding a finite unitary matrix by construction.
Lombardi's result for the classical approximation has ingredients that are
essential for MQDT to become the exact solution, but beyond that he uses
the approximation that the absolute value of the electron angular momentum
does not change. The latter approximation is not always good though it is
very convenient because the Poincaré section is then two-dimensional,
i. e. we can actually draw it. Yet this approximation is not
essential to the reinterpretation of MQDT as a QPM
The result has several interesting applications beyond the fact that it
affords a new understanding of MQDT.
First it can serve as a paradigm for a QPM and may even give a hint,
when and to what extent we really have to use semi-classics to construct a QPM.
Second the interpretation as a QPM allows for a much more stable
construction of eigen-values and eigen-functions of energy from the
unitary matrix given by the QPM.
Third the evolution of the eigen-phases as a function of energy is essential
to the possible transfer of properties of the eigen-phase spectrum to the
energy spectrum. This transfer is of basic interest for the understanding
of the relation of chaotic classical dynamics and random matrix theory, as
the latter is easier to understand for circular ensembles.
.
Prosen has proposed a very elegant unitarization of the QPM at the
price of obtaining an infinite dimensional matrix.
In our case the QPM is constructed directly from unitary transformations
between body fixed and space fixed frames as well as the phase shifts
typical of MQDT, thus yielding a finite unitary matrix by construction.
Lombardi's result for the classical approximation has ingredients that are
essential for MQDT to become the exact solution, but beyond that he uses
the approximation that the absolute value of the electron angular momentum
does not change. The latter approximation is not always good though it is
very convenient because the Poincaré section is then two-dimensional,
i. e. we can actually draw it. Yet this approximation is not
essential to the reinterpretation of MQDT as a QPM
The result has several interesting applications beyond the fact that it
affords a new understanding of MQDT.
First it can serve as a paradigm for a QPM and may even give a hint,
when and to what extent we really have to use semi-classics to construct a QPM.
Second the interpretation as a QPM allows for a much more stable
construction of eigen-values and eigen-functions of energy from the
unitary matrix given by the QPM.
Third the evolution of the eigen-phases as a function of energy is essential
to the possible transfer of properties of the eigen-phase spectrum to the
energy spectrum. This transfer is of basic interest for the understanding
of the relation of chaotic classical dynamics and random matrix theory, as
the latter is easier to understand for circular ensembles.
References
M.J. Seaton Rep. Prog. Phys. 48 (1983) 167 (and refs. therein)
E.B. Bogomolny, Nonlinearity 5 (1992) 805; Chaos 2 (1992) 5
T. Prosen, Physica D 91 (1996) 244
M. Lombardi, P. Labastie, M.C. Bordas and M. Broyer, J. Chem. Phys.
89 (1988) 3479
F. Leyvraz, M. Lombardi, R. Mendez-Sanchez and T.H. Seligman (to be published)
F. Leyvraz and T.H. Seligman,
in Proceedings of the fourth Wigner Symposium (1995);
Ed. N. Atakishiev et al., (World Scientific, Singapore 1996) P 350;
F. Leyvraz, R.A.
Mendez-Sanchez and T.H. Seligman (chao-dyn/9902009)
Rings: Generic structures of rotating systems
Thomas H. Seligman
Centro Internacional de Ciencias
and Centro de Ciencias Físicas, University of Mexico, UNAM,
Cuernavaca, México
From Galilieos discovery until a few years ago Saturns rings were a
singular phenomenon in the sky. This has radically changed since we
know that all major planets carry rings. This leads to the suspicion
that such ring structures are universal phenomena. Yet it is not
at all clear what universality class we look at.
In the present contribution we shall demonstrate that one of the two
universal scenarios for a sudden appearance upon variation of a
parameter of a localized manifold in
a Hamiltonian scattering system, will always lead to ring structures
if we deal with a system rotating around some point in space.
Consider free motion in a rotating frame: the particle will approach
the center of rotation up to the closest approach on a spiral
trajectory and then leave the central region on an outgoing spiral.
We now include a repulsive potential with convex potential contour lines
rotating with frequency 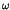 about a center that lies outside
the potential or at least its most repulsive part. The particle may
hit this potential on the ingoing or outgoing trajectory. In the
latter case the interaction may throw it onto another ingoing
trajectory. This will give opportunity for a second interaction if
the absolute value of the Jacobi-integral (Hamiltonian in the rotating
system) is not to large. This limitation results because otherwise the
particle leaves the region, where such an interaction is possible
before the center of interaction has swung around a sufficient angle.
Thus confined trajectories will appear as we reduce (or increase for
negative values) the Jacobi-integral.
There are two generic ways this can occur as a function of a
parameter. One is the sudden appearence of hyperbolic horseshoes with
infinite exponents. The other and the one we are interested in is
the saddle-center
bifurcation, which will give rise to stable periodic orbits in the
rotating frame. As these orbits are made up of slightly distorted
parts of a spiral they have ring shapes, and these non-circular
rings will have a precession with the frequency of rotation of the
system.
We shall use the model of a hard disc rotating about a center outside
of the disc to illustrate our general findings. This model has the
particular advantage that it does not allow for the alternate generic
scenario that we mentioned. A single disc will produce a wide ring
with a very involved structure, but the introduction of a second disc
moving on an inner circle with an incommensurable frequency will be
shown to produce narrow rings with structure.
about a center that lies outside
the potential or at least its most repulsive part. The particle may
hit this potential on the ingoing or outgoing trajectory. In the
latter case the interaction may throw it onto another ingoing
trajectory. This will give opportunity for a second interaction if
the absolute value of the Jacobi-integral (Hamiltonian in the rotating
system) is not to large. This limitation results because otherwise the
particle leaves the region, where such an interaction is possible
before the center of interaction has swung around a sufficient angle.
Thus confined trajectories will appear as we reduce (or increase for
negative values) the Jacobi-integral.
There are two generic ways this can occur as a function of a
parameter. One is the sudden appearence of hyperbolic horseshoes with
infinite exponents. The other and the one we are interested in is
the saddle-center
bifurcation, which will give rise to stable periodic orbits in the
rotating frame. As these orbits are made up of slightly distorted
parts of a spiral they have ring shapes, and these non-circular
rings will have a precession with the frequency of rotation of the
system.
We shall use the model of a hard disc rotating about a center outside
of the disc to illustrate our general findings. This model has the
particular advantage that it does not allow for the alternate generic
scenario that we mentioned. A single disc will produce a wide ring
with a very involved structure, but the introduction of a second disc
moving on an inner circle with an incommensurable frequency will be
shown to produce narrow rings with structure.
References
Planetary rings, R. Greenberg and
A. Brahic (eds.). The University of Arizona Press, Tucson (1984);
B.A. Smith, and the Voyager imaging team, Science 212
163 (1981); 215 504 (1982).
L. Benet, T.H. Seligman (submitted for publication)
N. Meyer et al., J. Phys A: Math. Gen.
28 2529 (1995).
M. Ding, et al.,
Phys. Rev. A 42, 7025 (1990); Phys Lett. A 153, 21
(1991).
T. Tél, C. Grebogi and E. Ott, Chaos
3 (1993) 495.
Complex trajectory description for
quantum tunnelling I
Akira Shudo
Department of Physics, Tokyo Metropolitan University,
Tokyo, Japan
Tunnelling phenomenon is one of the most familiar quantum
effects. The wavepacket in quantum mechanics can penetrate even into
the region where the classical trajectory cannot reach.
The barrier which prevents the transition to classically
forbidden regimes is always formed by the energy potential
in case of one degree of freedom system.
However, in higher dimension, in addition to the energy,
there sometimes appear dynamical barriers (KAM Tori) which are usually
coexisting with chaotic components in the phase space.
The classical trajectories are also confined dynamically if they
are placed in such regions initially. The quantum wavepacket can also
go over such dynamical barriers, and tunnelling penetration out of
dynamically formed barriers is called  dynamical tunnelling"
(Heller
dynamical tunnelling"
(Heller  Davis 1981, Bohigas, Tomsovic
Davis 1981, Bohigas, Tomsovic  Ullmo 1993, Creagh 1998).
The purpose of our talk is to show how the essential
difference between tunnelling in one dimension and that in more than
one-degree-of-freedom systems is explicitly understandable in terms of
the semiclassical methodology which has been elaborated extensively
in recent studies of quantum chaos. The main tool we will use
is the complex semiclassical theory in which not only usual real
classical orbits but also complex classical trajectories play a
key role in describing the purely quantum mechanical
phenomena such as tunnelling (Miller 1974).
We first introduce a simple model (kicked rotor), which is
suitably designed to test the dynamical tunnelling as purely as
possible and observe the time evolution of its wavefunction,
especially by focusing on the tunnelling tail.
The complex semiclassical analysis is then performed, aimed at
the interpretation of various features discovered in the tunnelling
wavefunction in chaotic systems.
The procedure of the complex semiclassical analysis is almost the same
as the real one, but in contrast with the real semiclassics,
finding a definite rule to select dominant complex
orbits becomes a crucial task, since in chaotic systems
there appear vastly many number of candidate complex
trajectories, all of which can contribute to the semiclassical propagator,
but not all of which contribute equally in weights.
The main message we will present in our first lecture is that
it is indeed possible to select such important complex orbits under
a certain rule, and the origin of various remarkable features
observed in the tunnelling tail in chaotic systems, which are completely
absent in integrable systems, can be explained by the group of complex
manifolds forming the chain-like structure
in the initial value representation of complex trajectories
(Shudo
Ullmo 1993, Creagh 1998).
The purpose of our talk is to show how the essential
difference between tunnelling in one dimension and that in more than
one-degree-of-freedom systems is explicitly understandable in terms of
the semiclassical methodology which has been elaborated extensively
in recent studies of quantum chaos. The main tool we will use
is the complex semiclassical theory in which not only usual real
classical orbits but also complex classical trajectories play a
key role in describing the purely quantum mechanical
phenomena such as tunnelling (Miller 1974).
We first introduce a simple model (kicked rotor), which is
suitably designed to test the dynamical tunnelling as purely as
possible and observe the time evolution of its wavefunction,
especially by focusing on the tunnelling tail.
The complex semiclassical analysis is then performed, aimed at
the interpretation of various features discovered in the tunnelling
wavefunction in chaotic systems.
The procedure of the complex semiclassical analysis is almost the same
as the real one, but in contrast with the real semiclassics,
finding a definite rule to select dominant complex
orbits becomes a crucial task, since in chaotic systems
there appear vastly many number of candidate complex
trajectories, all of which can contribute to the semiclassical propagator,
but not all of which contribute equally in weights.
The main message we will present in our first lecture is that
it is indeed possible to select such important complex orbits under
a certain rule, and the origin of various remarkable features
observed in the tunnelling tail in chaotic systems, which are completely
absent in integrable systems, can be explained by the group of complex
manifolds forming the chain-like structure
in the initial value representation of complex trajectories
(Shudo  Ikeda 1998).
Ikeda 1998).
References
Heller E.J. and Davis M.J. 1981 J. Chem. Phys. 75 246.
Creagh S.C. 1998 in Tunnelling in Complex Systems eds.
S. Tomsovic (World Scientific)35.
Bohigas, O., S. Tomsovic and D. Ullmo 1993 Phys. Rep. 223 45.
Miller W.H. and George T.F. 1974 Adv. Chem. Phys. 25 69.
Shudo A. and Ikeda K.S. 1998 Physica D 115 234.
Complex trajectory description for
quantum tunnelling II
Akira Shudo
Department of Physics, Tokyo Metropolitan University,
Tokyo, Japan
The subject of our second lecture is to present some theoretical backgrounds
for the semiclassical description of tunnelling in the presence of chaos,
especially to discuss the contributing and non-contributing problems
in the complex semiclassical approach.
In applying the complex semiclassical method,
we inevitably face the problem of how to select the contributing
complex (tunnelling) paths from all the candidates which satisfy
the saddle point condition in principle.
There would essentially be two distinct origins:
The first one is concerned with how to
find the most largely weighted complex paths among vastly many
complex candidates which should a priori be included
in the semiclassical superposition.
The weight of an individual contribution is almost determined by the
imaginary part of the action along each classical trajectory, and
the paths with large
imaginary actions may be negligible in the semiclassical sum.
This problem is purely classical, in particular it should be
solved in the context of the complex classical dynamics
(Milnor 1990).
We will show that the most relevant complex classical trajectories
in describing the tunnelling effect in chaotic systems are
very closely related to the Julia set in the corresponding
complex dynamical system.
More precisely, it can be shown that the Laputa chain, which
is the most important phenomenological object introduced
to explain all the features of tunnelling in chaotic systems,
is nothing but the intersection between the initial Lagrangian
manifolds and the complex stable manifolds of saddles in the Julia set
(Shudo  Ikeda 1999).
The second contributing and non-contributing problem arises from the
Stokes phenomenon in multi-dimensions.
The Stokes phenomenon is the discontinuous change of the asymptotic
solutions, and it occurs quite generically in the saddle point
method or the differential equation with large parameters.
Due to the Stokes phenomenon, not all of the complex
classical trajectories necessarily contribute to the final semiclassical
propagator.
Owing to the recent development of so-called exact WKB analysis which
allows us to treat asymptotic expansions on the analytical basis via
Borel-Laplace transform (Voros 1983),
the Stokes phenomenon now becomes well defined concept.
We will give a prescription for analyzing the Stokes phenomenon
in multi-dimensions, where the crossing of the Stokes curves is an essentially
new event while it is absent in 2nd-order differential equations.
It will be shown how the Riemann sheet structure of the Borel
transform(or
Ikeda 1999).
The second contributing and non-contributing problem arises from the
Stokes phenomenon in multi-dimensions.
The Stokes phenomenon is the discontinuous change of the asymptotic
solutions, and it occurs quite generically in the saddle point
method or the differential equation with large parameters.
Due to the Stokes phenomenon, not all of the complex
classical trajectories necessarily contribute to the final semiclassical
propagator.
Owing to the recent development of so-called exact WKB analysis which
allows us to treat asymptotic expansions on the analytical basis via
Borel-Laplace transform (Voros 1983),
the Stokes phenomenon now becomes well defined concept.
We will give a prescription for analyzing the Stokes phenomenon
in multi-dimensions, where the crossing of the Stokes curves is an essentially
new event while it is absent in 2nd-order differential equations.
It will be shown how the Riemann sheet structure of the Borel
transform(or  adjacency' in another context (Berry
adjacency' in another context (Berry 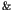 Howls 1991) ),
which is a crucial information in our exact WKB understanding of
the Stokes phenomenon, is determined by the Stokes graph
(Shudo
Howls 1991) ),
which is a crucial information in our exact WKB understanding of
the Stokes phenomenon, is determined by the Stokes graph
(Shudo 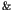 Ikeda 1999).
Ikeda 1999).
References
Milnor J. 1990 Introductory Lectures, SUNY at Stony Brook 1990/5.
Voros A. 1983 Ann. Inst. H. Poincar
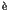 A 39 211.
A 39 211.
Berry M.V. and Howls. C.J. 1991 Proc. R. Soc. London 434 657.
Shudo A. and Ikeda K.S. 1999 to be published.
Critical bifurcation surfaces of discrete multi-dimensional
dynamics
Michael Sonis
Dept. of Geography, Bar-Ilan University, Israel
The purpose of this lecture is to construct the three-dimensional
analytical representation of the general procedure of linear local
bifurcation analysis developed in Sonis, 1993, on the basis of
classical Routh-Hurvitz conditions of asymptotic stability combined with
the movements of fixed point in the space of orbits. The bifurcation
phenomena are defined by the position of the boundaries of attraction of
the fixed point. It will be proven that the domain of attraction of the
fixed point of 3D discrete dynamics is bounded by three critical
bifurcation surfaces: the divergence surface corresponding to the case
in which one of the eigenvalues of the Jacobi matrix of the linear
approximation of the dynamics equals to 1; the flip surface
corresponding to the existence of the eigenvalue -1, and the flutter
surface corresponding to the pair of complex conjugated eigenvalues with
absolute values equal to 1. The crossing of these surfaces by the movement
of the fixed point will generate the plethora of all possible
bifurcation phenomena. This scheme of local bifurcation analysis will be
demonstrated by numerous application to bifurcation analysis of the
Henon map, the different examples of Socio-Spatial discrete Dynamics and
the theoretical example of the bifurcation analysis of the T. Puu
Dyopoly and Triopoly adjustment dynamics.
References
Dendrinos D S, Sonis M 1990. Chaos and Socio-Spatial Dynamics,
Springer Verlag Series of Applied Mathematics, vol. 86.
Sonis M, 1992. ``Behavior of Iterational Processes near the Boundary
of Stability Domain, with applications to the Socio-Spatial Relative
Dynamics". in Functional-Differential Equations, eds M. Drachlin
and E. Litsin 1 pp 198-227.
Nonlinear socio-ecological dynamics and first principles of
collective choice behavior of "Homo Socialis"
Michael Sonis
Dept. of Geography, Bar-Ilan University, Israel
Socio-ecological dynamics emerged from the field of Mathematical Social
Sciences and opened up avenues for re-examination of classical problems
of collective behavior in Social and Spatial sciences. The ``engine" of
this collective behaviour is the subjective mental evaluation of level
of utilities in the future, presenting sets of composite
socio-economic-temporal-locational advantages. These dynamics present
new laws of collective non-local multi-population behavior which are the
meso-level counterparts of the utility optimization in individual behavior.
The central core of the socio-ecological choice dynamics includes
the following first principle of the collective choice behavior of
``Homo Socialis" based on the existence of ``collective consciousness":
the choice behavior of ``Homo Socialis" is a collective meso-level choice
behavior such that the relative changes in choice frequencies depend on
the distribution of innovation alternatives between adopters of
innovations. This hypothesis expands essentially the view point of the
social statistical mechanics by including into the consideration the
collective conscience of ``human molecules", arising from the social
interactions and informational mass media effects.
The mathematical basis of the Socio-Ecological Dynamics includes two
mutually complemented analytical approaches both based on the use of
computer modeling as a theoretical and simulation tool. First approach
is the ``continuous approach" - the systems of ordinary and partial
differential equations reflecting the continuous time Volterra
ecological formalism in a form of antagonistic and/or cooperative
collective hyper-games between different sub-sets of choice
alternatives. Second approach is the ``discrete approach" - systems of
difference equations presenting a new branch of the non-linear discrete
dynamics - the Discrete Relative m-population/n-innovations
Socio-Spatial Dynamics (Dendrinos and Sonis, 1990). The generalization
of the Volterra mathematical formalism leads further to the meso-level
variational principle of collective choice behavior determining the
balance between the resulting cumulative social spatio-temporal
interactions among the population of adopters susceptible to the choice
alternatives and the cumulative equalization of the power of elites
supporting different choice alternatives. This balance governs the
dynamic innovation choice process and constitutes the dynamic meso-level
counterpart of the micro-economic individual utility maximization
principle.
The above described law of elite competition can be extended to each
many-dimensional iteration processes. Thus is the existence of the
extreme principle describing the discrete space-time transfer from the
past to the future. This principle represents the collective
synergetic interactions between the constituencies of the iteration
process. Moreover, this principle is the discrete time analog of the
law of meso-level variational principle of collective choice behavior
for the continuous time Socio-Ecological Dynamics.
References
Dendrinos D S, Sonis M 1990. Chaos and Socio-Spatial Dynamics,
Springer Verlag Series of Applied Mathematics, vol. 86.
Sonis M, 1992. ``Innovation Diffusion, Schumpeterian Competition and
Dynamic Choice: a New Synthesis". in Journal of Scientific &
Industrial Reseach, Special Issue on Mathematical Modelling of
Innovation Diffusion and Technological Change 51, no.3 pp172-186.
Impulses and waves in biological systems:
Exploring stability of membrane potential in excitable cells
C. Frank Starmer
Medical University of South Carolina,
Charleston, USA
Excitable cells are either stable or oscillate.
Subthreshold stimulation produces a transient departure from equilibrium
while suprathreshold stimulation produces a major deparation from
equilibrium that requires some time to return to the rest state.
The major electrical features of an excitable cell are an insulating cell
membrane and gated channels that permeate the membrane and control the flow
of ions down concentration gradients. A capacitor is formed by the cell
membrane surrounded by conducting fluid on either side while the gated
channels form non-linear resistors. The parallel combination of capacitors
and Na and K channels define a cellular reaction process which controls
the electrical ``state" of a cell. We explore the behavior of a simple
reaction diffusion process (Fitzhugh-Nagumo Model) of the form:
where
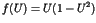 and
and
Phase plane analysis reveals the possibility of
two stable equilibria and 1 unstable equilibria, depending on medium properties.
The functions, f(U) and W are comparable to ionic currents that flow through
channels that penetrate the membrane of excitable cells.
By altering the channel conductances, the cell membrane potential will either be
stable or will oscillate. Genetic diseases, that alter the properties of
membrane ion channels can lead to shifts in the equilibrium of excitable
cells from stable to unstable. Epilepsy and the cardiac long QT syndrome
are two such examples. Experimental studies of membrane potential in
cardiac cells display shifts in equilibrium when treated with drugs that
block the flow of ions in membrane ion channels. This lecture will link
physical and mathematical models of excitable membranes and ion channel
blockade with the behavior of the minimal model (Fitzhugh-Nagumo)
and its associated phase
plane analysis of cellular stability and illustrate how genetic mutants of
ion channels lead to cardiac and cerebral arrhythmias that appear quite
complex.
References
Murray, J.D. 1993 Mathematical Biology 274-359, 1993. (Springer Verlag, Heidelberg)
274-359
Rinzel, J. and Terman, D.: Propagation phenomena in a bistable reaction-diffusion systems.
SIAM J. Appl. Math. 42 1111-1137, 1982.
Starmer, C.F.: Theoretical characterization of ion channel blockade: Ligand binding to periodically accessible receptors.
J. Theoretical Biology 119 235-249, 1986
Curran, M.E. et. al.: A molecular basis for cardiac arrhythmia: HERG mutations cause long QT syndrome. Cell
80 795-803, 1995.
Schroeder, B.C. et. al.: Moderate loss of function of cyclic-AMP-modulated KCNQ2/KCNQ3 K+ channels
causes epilepsy. Nature 396 687-690, 1999.
Impulses and waves in biological systems:
Exploring front formation and propagation
C. Frank Starmer
Medical University of South Carolina,
Charleston, USA
Isolated excitable cells are either stable or oscillate.
Diffusive coupling between excitable cells introduces a new property:
the spatial extent of the excitation must exceed a ``liminal" region that
is a function of media properties. In a uniform medium, fronts initiated
by excitation smaller than the liminal region will collapse while fronts
initiated by excitation of a region larger than the liminal region will
expand. We explore the behavior of a simple reaction diffusion
process of the form:
where
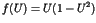 and
and
This lecture will focus on a number of interesting questions related for
formation and propagation of waves in an excitable medium, specifically
wave patterns associated with cardiac arrhythmias.
In homogeneous and uniform excitable media in the rest state,
there are two responses to stimulation:
if the stimulus is less than a critical value, a collapsing wave is initiated while
if the stimulus is greater than a critical value, and continuous expanding wave is
initiated. Under some conditions, it is possible to initiate a partial wave, i.e
a wave that expands in some directions and collapses in other directions.
Trailing a propagating wave is a region
known as the vulnerable region, where the non-uniformity
of the medium properties can result in incomplete front formation following
suprathreshold stimulation. Depending on the time and
location of stimulation after the passage of a wave, stimulation
results in either: 1) a
decaying front; 2) an expanding front; and 3) a wave fragment (wavelet) that expands
in some directions and collapses in other directions. In two and three
dimensional media,the wave fragment can evolve to a rotating spiral wave.
The duration of the period of vulnerability is
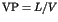 where
where  is the spatial extent of the suprathreshold stimulus
field and
is the spatial extent of the suprathreshold stimulus
field and  is the velocity of the conditioning wave . We will show that drugs that reduce the excitability of
isolated cells (classified as antiarrhythmic drugs) will increase the VP,
leading to dramatic increases in the rate of spontaneous and potentially
fatal arrhythmias. This new finding was confirmed in studies of
cardiac tissue.
is the velocity of the conditioning wave . We will show that drugs that reduce the excitability of
isolated cells (classified as antiarrhythmic drugs) will increase the VP,
leading to dramatic increases in the rate of spontaneous and potentially
fatal arrhythmias. This new finding was confirmed in studies of
cardiac tissue.
References
Murray, J.D. Mathematical Biology 274-359, 1993 (Springer Verlag, Heidelberg)
Rushton, W.A.H. Initiation of the propagated disturbance.
Proc R Soc Lond B 124 210-243, 1937.
Wiener, N. and Rosenblueth, A. The mathematical formulation of the problem of conduction
of impulses in a network of connected excitable elements, specifically in cardiac muscle.
Arch Inst Cardiol Mex 16 205-265, 1946.
Starmer, C.F. et. al. Vulnerability in an excitable medium: Analytical
and numerical studies of initiating unidirectional propagation. Biophysical
J. 65 1775-1787, 1993,
Starobin, J.M. et. al. Vulnerability in one-dimensional excitable media.
Physica D 70 321-341, 1994.
Starobin, J. and Starmer, C.F. A common mechanism links spiral wave meandering and
wavefront-obstacle separation. Phys. Rev. E 55 1193-1196, 1997.
Topics in nonlinear dynamics of the human cardiovascular system
Aneta Stefanovska
Group of Nonlinear Dynamics and Synergetics,
Faculty of Electrical Engineering, University of Ljubljana, Ljubljana,
Slovenia
We review the main results of analysis of time series measured
simultaneously at different sites of the human
cardiovascular system. Because our primary interest centres
on the dynamics of blood distribution, characteristics
during one cycle of blood through the system, which on average
takes about one minute, are considered.
First we discuss results of nonlinear time series
analysis with regard to system determinism and complexity. The
analysis in the time domain and in the phase space revealed
highly deterministic and almost conservative nature of cardiovascular
control system on time scale of minutes
(Stefanovska and Krošelj, 1997, Bracic and Stefanovska,
1998a, Stefanovska and Bracic, 1999a, 1999b).
Then we present results of time-frequency analysis.
The wavelet transform, a method with logarithmic
frequency resolution, was used to study oscillations in
cardiovascular signals (Bracic and Stefanovska, 1998b,
Kvernmo, Stefanovska, Bracic, Kirkeboen and Kvernebo, 1998,
Stefanovska, Bracic and Kvernmo, in print).
The heart rate variability (HRV), derived from the signal resulting
from electrical activity of the heart (ECG), bears the variations
of instantaneous heart rate and RR intervals in the ECG. Several
central and peripheral oscillators contribute to the variations
between subsequent heart beats. Analysis of signals measured from
respiration, cardiac function and blood flow, all revealed the
existence of five almost periodic frequency components, illustrating
that all the cardiac periodicities are propagated
as traveling waves.
The physical description of the cardiovascular control system
depends essentially on the current understanding of physiological
origin of observed oscillations. The evidence that endothelial
activity is manifested as oscillations in blood flow with a
characteristic frequency of around 0.01Hz was recently
demonstrated (Stefanovska, Bracic and Kvernmo, in print).
The mode of changes in the characteristics of oscillations with
aging, physical activity, diabetes, after myocardial infarction,
or general anaesthesia also provides insight into the physiological
and physical characteristics of the system. In addition,
the strength of phase and frequency couplings among
the oscillations, modified in different states of the
cardiovascular system, is discussed.
References
Stefanovska A and Krošelj P 1997 Open Sys. Information Dyn.
4
457
Bracic M and Stefanovska A 1998a Bull. Math. Biol. 60 417
Stefanovska A and Bracic M 1999a Contemporary Physics
40 31
Stefanovska A and Bracic M 1999b Control Engineering
Practice
7 161
Bracic M and Stefanovska A 1998b Bull. Math. Biol. 60 919
Kvernmo HD, Stefanovska A, Bracic M, Kirkebøen K-A and
Kvernebo K, 1998 Microvascular Research 56 173
Stefanovska A, Bracic M, Kvernmo HD IEEE Trans. Biomed.
Eng. In press.
Cardiorespiratory interactions
Aneta Stefanovska
Group of Nonlinear Dynamics and Synergetics,
Faculty of Electrical Engineering, University of Ljubljana, Ljubljana,
Slovenia
Oscillators that have a standard waveform and amplitude to which
they return after small perturbation are known as limit-cycle
oscillators. They incorporate a dissipative mechanism to dump
oscillations that grow too large and source of energy to pump up
those that become too small. Coupled, they
continuously perturb each other and everyone of them permanently
tends toward a limit cycle with time-varying amplitude
and characteristic frequency.
Signals derived from the
human cardiovascular system have been found to contain several periodic
components (Akselrod et al, 1981), thereby raising the question
of whether the blood distribution system and its regulatory mechanisms
can be described as a set of coupled oscillators
(Stefanovska and Bracic, 1999).
On minute time scale the peripheral blood flow was shown to contain five
characteristic frequencies (Bracic and Stefanovska, 1998). The
physiological origin of two of them is easy to evidence by simultaneous
measurements of the heart and respiratory activity. The heart rate at
rest
ranges from 0.6 Hz in sportsmen to 1.6 Hz in subjects with impaired
cardiovascular systems and the respiratory frequency from 0.15 Hz
to 0.35 Hz. As early as 1733, Hales observed that changes in heart
rate were related in a regular manner to the respiratory pattern,
and in 1847 Ludwig documented that the heart rate increased on
inspiration and decreased on expiration. The respiratory modulation
of the heart rate, known as ``respiratory sinus arrhythmia", raises
questions
not answered so far: how strongly those two systems are coupled, how
strongly they modulate each others amplitudes and characteristic
frequencies, does phase synchronisation exist at rest in healthy and
diseased states? Raschke (1987) analysed effects of mutual interactions
and demonstrated that during sleep inspiration starts preferably at a
certain phase of the cardiac cycle. Glass and Mackey (1988)
concluded that they are weakly coupled and generally not phase
locked. In contrast, Rosenblum et al (1998) revealed hidden
phase-locked regimes between the cardiac and the respiratory
rhythms.
We discuss mutual frequency and amplitude modulation of the
heart and respiratory cycles. The couplings are not symmetrical,
the respiratory system is imposing stronger influence to the cardiac
system than vice versa. The other three oscillatory processes
involved in the regulation of blood distribution system also influence
the heart and respiratory activity. Consequently, a stable phase
locking among those two oscillators can not be obtained in healthy
cardiovascular system. In addition, we present states of coupling
between the two oscillatory systems modified by aging, diabetes,
myocardial infarction, or general anaesthesia.
References
Axelrod S et al 1981 Science 213 220
Stefanovska A and Bracic M 1999 Contemporary Physics
40 31
Bracic M and Stefanovska A 1998 Bull. Math. Biol. 60
919
Hales S 1773 Statical Essays II, Haemastaticks, (London:
Innings Manby)
Ludwig C 1847 Arch Anat Physiol 13 242
Raschke F 1987 in ``Temporal Disorder in Human Oscillatory
Systems", eds. L Rensing, U an der Heiden and MC Mackey, (Berlin:
Springer) pp152-158
Glass L and Mackey MC 1988 From Clocks to Chaos: The Rhythms of
Life,
(Princeton: Princeton UP)
Rosenblum M et al 1998 IEEE Mag Eng Med Biol
November/December 46
Nonlinear dynamics, bifurcation, and symmetry
Ian Stewart
Mathematics Institute,
University of Warwick
Coventry, UK
In many applications of nonlinear dynamics, the model system
possesses a degree of symmetry. Symmetry affects the
`generic' behaviour of the system, and its presence
should be taken into account when analysing the predictions
of the model.
The course will provide a three-lecture introduction to
some basic
theory, including fundamental existence theorems for
the existence of symmetry-breaking
These include criteria for the existence of symmetry-breaking branches of
steady and periodic states, and some basic concepts related to
`symmetric chaos'. We emphasize the role of symmetry as a
general framework for such problems.
Summary of Course Structure
- Steady State Bifurcation
Invariant functions and equivariant mappings. Group actions,
isotropy subgroups, fixed-point spaces. The isotropy
lattice. Genericity of absolutely irreducible representations.
The Equivariant Branching Lemma.
Examples:
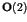 -symmetric systems,
-symmetric systems,
 -symmetric systems
-symmetric systems
 -symmetric systems.
Applications: Speciation, convection, Taylor-Couette flow.
-symmetric systems.
Applications: Speciation, convection, Taylor-Couette flow.
- Hopf Bifurcation to Periodic States
Loop space, circle group action by phase shift,
spatio-temporal symmetries. Liapunov-Schmidt reduction.
Genericity of
 -simple representations.
The Equivariant Hopf Theorem.
Examples:
-simple representations.
The Equivariant Hopf Theorem.
Examples:  -symmetric systems,
-symmetric systems,
 -symmetric systems.
Applications: Oscillating hosepipe, animal locomotion, convection.
-symmetric systems.
Applications: Oscillating hosepipe, animal locomotion, convection.
- Symmetric Chaos
Pointwise and setwise symmetry of an attractor. Symmetry
on average. Detectives. Collisions of attractors.
Transverse Liapunov exponents.
Examples: The cubic logistic map,
 -symmetric maps.
Applications: Oscillator arrays, the Faraday Experiment.
-symmetric maps.
Applications: Oscillator arrays, the Faraday Experiment.
1. Steady State Bifurcation
Steady state bifurcation occurs when an equilibrium of a dynamical
system becomes unstable as a parameter 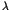 is varied.
In suitable circumstances, the generic result is the creation
of a branch of `new' equilibria. We study such behaviour
when the dynamical system has symmetry.
Specifically, by ` has symmetry' we mean the following.
Let
is varied.
In suitable circumstances, the generic result is the creation
of a branch of `new' equilibria. We study such behaviour
when the dynamical system has symmetry.
Specifically, by ` has symmetry' we mean the following.
Let 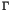 be a Lie group of linear transformations of
be a Lie group of linear transformations of
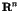 .
We say that
.
We say that 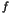 is
is
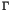 -equivariant if
-equivariant if
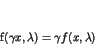 |
(5) |
for all
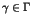 .
Consider a
.
Consider a  -equivariant ODE
-equivariant ODE
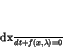 |
(6) |
where
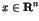 ,
,
 . For simplicity, assume that
. For simplicity, assume that
 , so there exists a `trivial branch' of solutions
, so there exists a `trivial branch' of solutions
 . The linearization of
. The linearization of 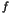 is
is
Local bifurcation at 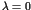 occurs when the trivial branch undergoes a
change of linear stability, so that
occurs when the trivial branch undergoes a
change of linear stability, so that  has eigenvalues on the imaginary
axis (often called critical eigenvalues).
There are two cases:
has eigenvalues on the imaginary
axis (often called critical eigenvalues).
There are two cases:
- Steady-state bifurcation:
 has a zero eigenvalue.
has a zero eigenvalue.
- Hopf bifurcation:
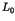 has a complex conjugate pair of eigenvalues
has a complex conjugate pair of eigenvalues
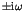 .
.
In the first lecture we look at steady-state bifurcation. The
central result here is the Equivariant Branching Lemma,
which asserts the existence of branches of equilibria with
certain kinds of symmetry.
The basic examples are
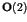 -symmetric systems,
-symmetric systems,
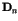 -symmetric systems,
and
-symmetric systems,
and
 -symmetric systems. Here
-symmetric systems. Here  is the orthogonal
group in the plane,
is the orthogonal
group in the plane,
 is the dihedral group,
and
is the dihedral group,
and
 is the symmetric group of degree
is the symmetric group of degree 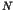 .
Applications include speciation in evolutionary
systems (modelled as a dynamic on phenotypic space),
convection, and Taylor-Couette flow of a fluid
between rotating cylinders.
.
Applications include speciation in evolutionary
systems (modelled as a dynamic on phenotypic space),
convection, and Taylor-Couette flow of a fluid
between rotating cylinders.
2. Hopf Bifurcation
Hopf bifurcation leads to a branch of time-periodic
solutions. It is analogous to steady-state
bifurcation, but now there is an
extra symmetry given by an action of the circle group.
Intuitively, this represents shifting the phase of a solution.
The problem becomes
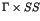 -equivariant.
The analogue of the Equivariant Branching Lemma is the
Equivariant Hopf Theorem. It is proved by posing the
problem on
loop space -- a Banach space of periodic
functions -- upon which there is a circle group action by phase shift,
corresponding to
spatio-temporal symmetries.
Applications include
the oscillating hosepipe of circular cross-section,
with both standing and rotating waves; animal locomotion,
where the patterns with which animals move their legs when
they walk, trot, run, and so on can be classified and
organised; and convection.
-equivariant.
The analogue of the Equivariant Branching Lemma is the
Equivariant Hopf Theorem. It is proved by posing the
problem on
loop space -- a Banach space of periodic
functions -- upon which there is a circle group action by phase shift,
corresponding to
spatio-temporal symmetries.
Applications include
the oscillating hosepipe of circular cross-section,
with both standing and rotating waves; animal locomotion,
where the patterns with which animals move their legs when
they walk, trot, run, and so on can be classified and
organised; and convection.
3. Symmetric Chaos
Symmetric systems can have chaotic attractors, and here
the symmetry of the attractor represents the symmetry
`on average' over long periods of time of the
corresponding states. It is important to distinguish
between
pointwise and setwise symmetry of an attractor.
The symmetry of an attractor can be found
experimentally by using the theory of `detectives'.
Important phenomena include
collisions of attractors, in which conjugate versions
of a chaotic attractor can suddenly merge, with a change
of symmetry.
Examples include the cubic logistic map
and
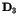 -symmetric maps.
Applications include chaotic dynamics
of oscillator arrays, synchronisation of
coupled chaotic oscillators, and the Faraday Experiment,
in which a dish of fluid is vibrated in the vertical direction.
-symmetric maps.
Applications include chaotic dynamics
of oscillator arrays, synchronisation of
coupled chaotic oscillators, and the Faraday Experiment,
in which a dish of fluid is vibrated in the vertical direction.
References
Ashwin P, Buescu J, Stewart I 1994 Bubbling of attractors and
synchronization of chaotic oscillators, Phys. Lett. A 193
126-139.
Ashwin P, Buescu J, Stewart I 1996 From attractor to chaotic saddle:
a tale of transverse instability, Nonlinearity 9
703-737.
Buescu J, Stewart I 1995 Liapunov stability and adding machines,
Ergod. Th. & Dynam. Sys. 15 271-290.
Cohen J, Stewart I 2000 Polymorphism viewed as phenotypic symmetry-breaking,
in Nonlinear Phenomena in Physical and Biological Sciences
(ed. Malik S K),
Indian National Science Academy, New Delhi
(World Mathematical Year 2000), to appear.
Collins J J, Stewart I 1993 Hexapodal gaits and coupled nonlinear
oscillator models, Biol. Cybern. 68 287-298.
Collins J J, Stewart I 1993 Coupled nonlinear oscillators and the
symmetries of animal gaits, J. Nonlin. Sci. 3 349-392.
Dellnitz M, Golubitsky M, Stewart I, Hohmann A 1995 Spirals in
scalar reaction-diffusion equations, Internat. J. Bif. Chaos
5 1487-1501.
Dionne B, Golubitsky M, Stewart I 1996
Coupled cells with internal symmetry:
I. Wreath products, Nonlinearity 9 559-574.
Dionne B, Golubitsky M, Stewart I 1996
Coupled cells with internal symmetry:
II. Direct products, Nonlinearity 9 575-599.
Dionne B, Golubitsky M, Silber M, Stewart I 1995 Time-periodic
spatially-periodic planforms in Euclidean equivariant PDE,
Phil. Trans. Roy. Soc. London A 352 125-168.
Golubitsky M, Field M 1992 Symmetry in Chaos Oxford
University Press, Oxford.
Golubitsky M, Knobloch E, Stewart I 1999 Target patterns and spirals
in planar reaction-diffusion systems, Research report UH/MD-256,
University of Houston.
Golubitsky M, Schaeffer D G 1985 Singularities and Groups in
Bifurcation Theory vol.1, Springer-Verlag, New York.
Golubitsky M, Stewart I 1985 Hopf bifurcation in the presence of
symmetry, Arch. Rational Mech. Anal. 87 107-165.
Golubitsky M, Stewart I 1986 Symmetry and stability in Taylor-Couette
flow, SIAM J. Math. Anal. 17 249-288.
Golubitsky M, Stewart I 1986 Hopf bifurcation with dihedral group symmetry:
coupled nonlinear oscillators, in Multiparameter Bifurcation
Theory (eds. Golubitsky M, Guckenheimer J), Proceedings of
the AMS-IMS-SIAM Joint Summer Research Conference, July 1985,
Arcata; Contemporary Math. 56 Amer. Math.
Soc. Providence RI 131-173.
Golubitsky M, Stewart I, Collins J J, Buono L 1998 A modular network
for legged locomotion, Physica D 115 56-72.
Golubitsky M, Stewart I 1999 Symmetry and pattern formation in
coupled cell networks, Proceedings of IMA Conference on
Pattern Formation 1998 to appear.
Golubitsky M, Stewart I, Schaeffer D G 1988 Singularities and Groups in
Bifurcation Theory vol.2, Springer-Verlag, New York.
King G, Stewart I 1992 Symmetric chaos,
in Nonlinear Equations in the Applied
Sciences (eds. Ames W F, Rogers C) Academic Press London
257-315.
Stewart I 1987 Stability of periodic solutions in symmetric
Hopf bifurcation, Dynam. Stab. Sys. 2 149-166.
Stewart I 1988 Bifurcations with symmetry, in New Directions in Dynamical
Systems (eds. Bedford T, Swift J W), London Math. Soc. Lecture
Notes 127 Cambridge Univ. Press 235-283.
Stewart I 1992 Bifurcation theory old and new, in Dynamics of Numerics and
Numerics of Dynamics (eds. Broomhead D S, Iserles A)
IMA Conference Series 34 Oxford University Press 31-67.
Stewart I 1992 Broken symmetry and the formation of spiral patterns in fluids,
in Spiral Symmetry (eds. Hargittai I, Pickover C A),
World Scientific, Singapore 187-220.
Microwave studies of chaotic billiards and disordered systems
Hans-Jürgen Stöckmann
Fachbereich Physik der Philipps-Universität,
Marburg, Germany
Chaotic billiards are ideal model systems to study the quantum mechanical
properties of classically chaotic systems. Billiards with hard walls are
conceptionally particularly simple. The classical trajectories can be
calculated elementarily, and the Schrödinger equation reduces to the free
wave equation with Dirichlet boundaries at the walls. Nevertheless the
calculations soon become elaborately, in particular, if spectra or wave
functions are to be determined in dependence of one external parameter,
usually the billiard length or the position of an inserted scatterer. Here
analogous experiments are an interesting alternative. They make use of the
equivalence of the stationary Schrödinger equation, and the
time-independent wave equation, the Helmholtz equation. In two-dimensional
microwave billiards this equivalence is complete, including the boundary
conditions.
After a short introduction into the problematic of the quantum mechanics of
classically chaotic systems, shortly termed `quantum chaos', different
types of billiard experiments are introduced. The main part of the talk is
devoted to microwave billiards. Results on global and local billiard
spectral level dynamics are presented as well as measurements in
three-dimensional chaotic microwave resonators. Here the equivalence
between Schrödinger equation and electromagnetic wave equation does no
longer hold. The talk ends with a discussion of transmission and
localization in disordered systems.
References
Stöckmann H J and Stein J 1990
Phys. Rev. Lett. 64 2215
Sridhar S 1991
Phys. Rev. Lett. 67 785
Stein J and Stöckmann H J 1992
Phys. Rev. Lett. 68 2867
Gräf H D et al. 1992
Phys. Rev. Lett. 69 1296
So P et al. 1995
Phys. Rev. Lett. 74 2662
Stein J et al. 1995
Phys. Rev. Lett. 75 53
Kudrolli A et al. 1995
Phys. Rev. Lett. 75 822
Ellegaard C et al. 1995
Phys. Rev. Lett. 75 1546
Stöckmann H J 1999
Quantum Chaos - An Introduction, Cambridge university press
Microwave billiards as scattering systems
Hans-Jürgen Stöckmann
Fachbereich Physik der Philipps-Universität,
Marburg, Germany
It is impossible to study a system without disturbing it by the measuring
process. To determine, e. g., the spectrum of a microwave billiard, we have
to drill a hole into its wall, introduce a wire, and irradiate a microwave
field. Due to the presence of the antenna a rectangular microwave cavity,
e. g., is no longer integrable, but has become pseudointegrable.
The measurement thus unavoidably yields an unwanted combination of the
system's own properties and those of the measuring apparatus. The
mathematical tool to treat the coupling between the system and the
environment is provided by scattering theory, which has originally been
developed in nuclear physics. Later this theory has been successfully applied to mesoscopic systems and microwave billiards as well.
In this talk scattering theory will be applied to billiard systems, resulting
in the billiard equivalent of the Breit-Wigner function, well-known from
nuclear physics for many years. The consequences of the coupling for the
spectral statistics will be discussed, as well as for resonance depths and
widths. In the last part results on transmission through billiards with open
channels are presented. Here we have a close correspondence to mesoscopic
systems, which can be linked to scattering theory via the Landauer formula
expressing the conduction through mesoscopic devices in terms of
transmission probabilities.
References
Lewenkopf C H and Weidenmüller H A 1991
Ann. Phys. 212 53
Alt H et al. 1995
Phys. Rev. Lett. 74 62
Stoffregen U et al. 1995
Phys. Rev. Lett. 74 1995
Stein J et al. 1995
Phys. Rev. Lett. 75 53
Lehmann N et al. 1995
Nucl. Phys. A 583 223
Alt. H et al. 1996
Phys. Lett. B 366 7
Haake F et al. 1996
J. Phys. A 29 5745
Stöckmann H J and Šeba P 1998
J. Phys. A 31 3439
Stöckmann H J 1999
Quantum Chaos - An Introduction, Cambridge university press
Phase resetting in medicine and biology -
Stochastic approach and applications
Peter A. Tass
Department of Neurology,
Heinrich-Heine-University, Düsseldorf, Germany
Synchronization processes are of great importance in several branches of
science, e.g., in biology, medicine and physics.
We present a new theoretical approach to phase resetting and
stimulation-induced synchronization and desynchronization in a population
of interacting oscillators in the presence of noise (Tass 1999).
The theoretical investigations of spontaneously emerging dynamics of
populations of interacting oscillators have revealed numerous significant
results (Kuramoto 1984). From the standpoint of neuroscience, however,
there is still an enormous need for theoretical studies addressing
stimulation-induced transient synchronization and desynchronization processes.
The impact of stimuli on synchronized neuronal oscillators is of great
importance for the study of brain functioning
(Steriade, Jones, Llinás 1990, Singer, Gray 1995, Hari, Salmelin 1997)
and of therapeutic stimulation techniques in neurology and neurosurgery
(Benabid et al. 1991, Blond et al. 1992).
In Winfree's (1980) pioneering topological approach to phase
resetting the influence of noise and synchronizing couplings was neglected.
For this reason with methods from synergetics (Haken 1983) and statistical
mechanics we, first, study patterns of synchrony emerging in the presence
of noise (Kuramoto 1984, Tass 1999). Second, the impact of periodic and,
in particular, single pulsatile stimuli on different synchronized states
is investigated in detail (Tass 1999).
We encounter a variety of characteristic stimulation-induced dynamical
features, for instance, different sorts of transient desynchronization and
resynchronization processes. Moreover, data analysis tools are presented
which enable us to apply the theory to design and evaluate stimulation
experiments. Finally, we propose improvements to stimulation
techniques as used by neurologists and neurosurgeons in the context of
Parkinson's disease (Tass 1999).
References
Benabid A L et al. 1991 The Lancet 337, 403
Blond S et al. 1992 J. Neurosurg. 77, 62
Haken H 1983 Advanced Synergetics,
(Berlin: Springer)
Hari R, Salmelin R 1997 TINS 20, 44
Kuramoto Y 1984 Chemical Oscillations, Waves, and Turbulence
(Berlin: Springer)
Singer W, Gray C M 1995 Annu. Rev. Neurosci. 18, 555
Steriade H, Jones E G, Llinás R 1990
Thalamic Oscillations and Signaling (New York: John Wiley & Sons)
Tass P A 1999 Phase Resetting in Medicine and Biology - Stochastic
Modelling and Data Analysis (Berlin: Springer) (will appear in May 1999)
Winfree A T 1980 The Geometry of Biological Time
(Berlin: Springer)
Detection of cerebral synchronization processes
Peter A. Tass
Department of Neurology,
Heinrich-Heine-University, Düsseldorf, Germany
Synchronization of neuronal oscillatory activity is important under both
physiological and pathological conditions. For instance, according to animal
experiments synchronization appears to be a basic mechanism for coordinating
different neuronal populations during complex tasks like visual pattern
recognition (Singer, Gray 1995) and motor control (Roelfsema et al. 1997). By
means of magnetoencephalography (MEG) and electroencephalography (EEG)
the cerebral activity can noninvasively be measured in humans
(Hämäläinen et al. 1993). To study synchronization processes of this
kind in humans two data analysis tools (Tass et al. 1998, Tass 1999) were
developed which are applied to MEG data or EEG data or directly to the
cerebral current density obtained by suitable inverse methods (cf.
Hämäläinen et al. 1993).
The first method makes it possible to detect 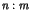 phase synchronization
in noisy non-stationary data (Tass et al. 1998). It is designed for detecting
self-synchronization in terms of an adjustment of the rhythms of ongoing
oscillations. To this end a sliding window analysis is performed, where one
needs a window length corresponding to at least eight to ten periods of the
oscillation. This method was developed based on the concept of phase
synchronization of chaotic oscillators (Rosenblum, Pikovsky, Kurths 1996,
Pikovsky, Rosenblum, Kurths 1996).
The second method aims at analyzing short-term synchronization processes which
are induced by a stimulus (Tass 1999). Accordingly, it is designed to detect
so-called stimulus-locked
phase synchronization
in noisy non-stationary data (Tass et al. 1998). It is designed for detecting
self-synchronization in terms of an adjustment of the rhythms of ongoing
oscillations. To this end a sliding window analysis is performed, where one
needs a window length corresponding to at least eight to ten periods of the
oscillation. This method was developed based on the concept of phase
synchronization of chaotic oscillators (Rosenblum, Pikovsky, Kurths 1996,
Pikovsky, Rosenblum, Kurths 1996).
The second method aims at analyzing short-term synchronization processes which
are induced by a stimulus (Tass 1999). Accordingly, it is designed to detect
so-called stimulus-locked 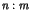 transients which are stimulus locked epochs
displaying a stereotyped time course of the
transients which are stimulus locked epochs
displaying a stereotyped time course of the 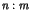 phase difference (with and
without conduction delay) (Tass 1999). Its time resolution reaches down to
the millisecond range, and, hence, this method can cope with short synchronous
epochs which are important in the context of cerebral information processing.
This data analysis tool originates from the theoretical approach to
phase resetting and stimulation-induced synchronization and desynchronization
in clusters of interacting oscillators which was presented in the first lecture.
The two methods provide us with complementary information concerning
spontaneously emerging synchronization as well as stimulus-induced
synchronous epochs. Analyzing the two types of synchronization in MEG and
EEG data opens up new and promising possibilities for the study of brain
functioning. Theory and physiological applications are presented in detail.
phase difference (with and
without conduction delay) (Tass 1999). Its time resolution reaches down to
the millisecond range, and, hence, this method can cope with short synchronous
epochs which are important in the context of cerebral information processing.
This data analysis tool originates from the theoretical approach to
phase resetting and stimulation-induced synchronization and desynchronization
in clusters of interacting oscillators which was presented in the first lecture.
The two methods provide us with complementary information concerning
spontaneously emerging synchronization as well as stimulus-induced
synchronous epochs. Analyzing the two types of synchronization in MEG and
EEG data opens up new and promising possibilities for the study of brain
functioning. Theory and physiological applications are presented in detail.
References
Hämäläinen M et al. 1993 Rev. Mod. Phys. 65, 413
Pikovsky A S, Rosenblum M G, Kurths J 1996
Europhys. Lett. 34, 165
Roelfsema P R et al. 1997 Nature 385, 157
Rosenblum M G, Pikovsky A S, Kurths J 1996 Phys. Rev. Lett.
76, 1804
Singer W, Gray C M 1995 Annu. Rev. Neurosci. 18, 555
Tass P A 1999 Phase Resetting in Medicine and Biology - Stochastic
Modelling and Data Analysis (Berlin: Springer) (will appear in May 1999)
Tass P et al. 1998 Phys. Rev. Lett. 81, 3291



Next: SHORT REPORTS
Up: programme
Previous: INVITED LECTURERS AND SPEAKERS