Ladder operator formalisms typically arise in factorization approaches to Schrödinger operators. There, they serve to an algebraic understanding of spectral problems like finding suitable eigenvalues of the linear operators under consideration. Also when it comes to describing supersymmetric Schrödinger operators in quantum mechanics, the concept of lowering and raising operators turns out to have an important meaning. So far, typical scenarios when ladder operators arise are briefly sketched. In recent contributions it has become apparent that methods involving ladder operators can also be used to deal with moment problems in context of special functions in analysis. We give several examples for this application. It remains a fascinating task and also a kind of challenge to investigate the interactions between related analytic and stochastic structures. For instance, the role of discrete Hermite polynomials and their connections with discrete martingale theory has to be understood in detail.
References
C. Berg, A. Ruffing: Generalized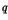 
-Hermite Polynomials, Communications in Mathematical Physics 223, (2001), 29-46
Z. Brzezniak, T. Zastawniak: Basic Stochastic Processes, Springer Undergraduate Mathematics Series, Springer, Berlin-Heidelberg-New York (1999)
T. S. Chihara: An introduction to orthogonal polynomials, Gordon and Breach, New York-London-Paris (1978)
P. J. Fitzsimmons: Hermite Martingales, to appear in the Séminaire de Probabilité
W. Hackenbroch, A. Thalmaier: Stochastische Analysis, Teubner, Stuttgart, (1994)
M.E.H. Ismail, M. Rahman: The 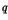-Laguerre Polynomials and Related Moment Problems, J. Math. Anal. Appl. 218 (1998), 155-174
R. Lasser, A. Ruffing: Continuous Orthogonality Measures and Difference Ladder Operators for Discrete 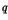-Hermite Polynomials II, preprint (2002)
A. Plucinska: A stochastic characterization of Hermite polynomials, J. Math. Sci. 89 (1998), 1541-1544
M. Reed, B. Simon: Methods of Modern Mathematical Physics, vol. 4, Analysis of Operators, Academic Press, Inc., San Diego (1994)
A. Ruffing: Lattice Quantum Mechanics and Difference Operators for Discrete Oscillator Potentials, Shaker Verlag, Aachen (1999)
B. Simon: The classical moment problem as a self-adjoint finite difference operator, Advances in Math. 137 (1998), 82-203