Intermediate quantum-level statistics by means of quaternion representation of distributions

Hiroshi Hasegawa

Institute of Quantum Science, Nihon University,
Chiyoda-ku, Tokyo 101-8308, Japan

There has been a long-standing subject in quantum-chaos studies to achieve a framework of energy-level statistics which interplolates between Poisson for integrable systems and those of Gaussian random matrix ensembles (GOE, GUE and GSE) for fully chaotic systems by means of a parameter [1]. In 1985, Yukawa [2] gave an excellent idea to construct such a one-parameter family of $N$-level distributions, based on the so-called level dynamics [3]: one considers an $N \times N$ Hermitian matrix of the form $H=H_0+tV$ (a perturbation of $H_0$ by another $V$ with perturbation strength $t$ which is regarded as the``time''). His result can be summarized by a special form

$$P_{N,\beta}(x_1,x_2,..,x_N) = C_{N,\beta}\prod_{j<k}\left( \... ..., \, \, 2 \, \, {\rm GUE}, \, \, 4 \, \, {\rm GSE}. \eqno{(1)}$$

Here, the parameter that appears is $a$ which interpolates the two limits as

$$a \to 0 \quad {\rm Poisson \, \, limit}, \qquad a \to \infty \quad {\mbox{ Gaussian limit (Wigner-Dyson limit).}} \eqno{(2)}$$

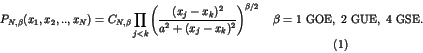
A further treatment of the distribution (1) to deduce concrete statistics (the spacing distribution, long-range 2-level correlations, etc.) is a hard problem, and have so far produced little fruits. However, for the unitary symmetry class $\beta=2$, a fully analytic method was devised by Forrester [4]: he showed that for this class expression (1) can be rewritten as a determinant

$$W_N^{(\beta=2)}(x_1,..,x_N) \equiv a^{-N}\prod_{1\le j<k\le ... ...\left[ \frac{1}{a-i(x_j-x_k)} \right]_{j,k=1,..,N}, \eqno{(3)}$$

where the right-hand side allows an infinite sum over $N$ with coefficient $\zeta$, called the grand canonical series with fugacity $\zeta$. In the present talk, it will be extended to the other two classes i.e. orthogonal and symplectic classes by using quaternion representation [5] which replaces the two opposite limits in (2) by $\zeta \to 0$ and $\zeta \to \infty$, respectively. It is based on our recent work [6].

References
[1] For example, A.D. Mirlin, Phys. Rep. 326(2000), 259.
[2] T. Yukawa, Phys. Rev. Lett. 54(1985), 1883; Phys. Lett. A 116(1986), 227; A 245(1998), 183.
[3] F. Haake, Quantum Signature of Chaos, Springer Verlag, Berlin, New York (1991).
[4] P.J. Forrester, Phys. Lett. A 173(1993), 355.
[5] F.J. Dyson, Comm. Math. Phys. 19(1970), 235.
[6] H. Hasegawa and Y. Sakamoto, Grand canonical random matrices for intermediate level statistics, Phys. Lett. A 297(2002), 146.